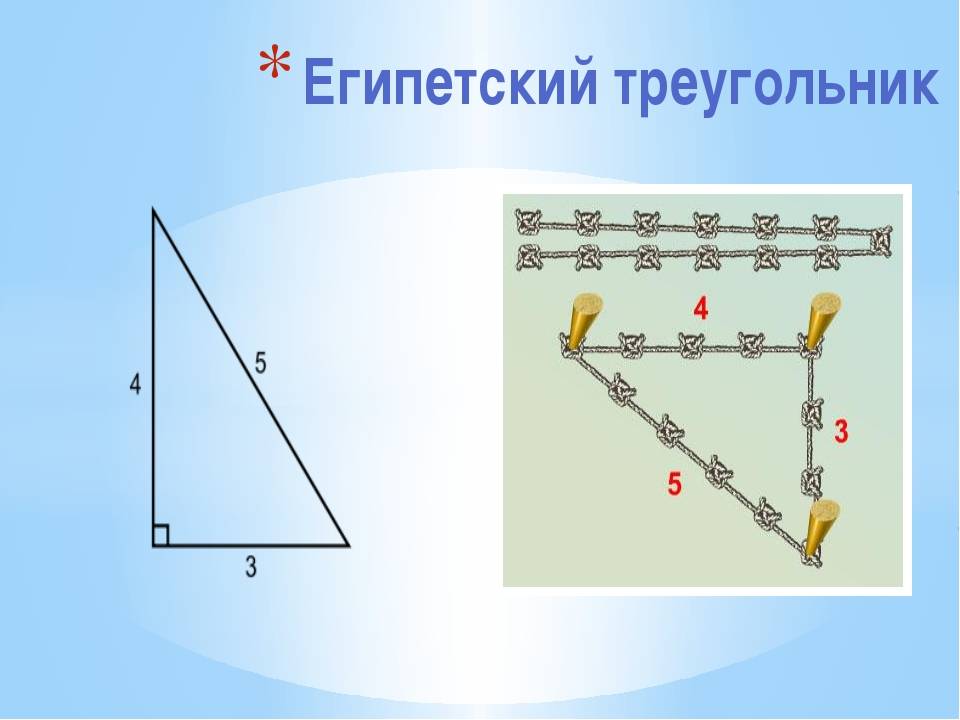
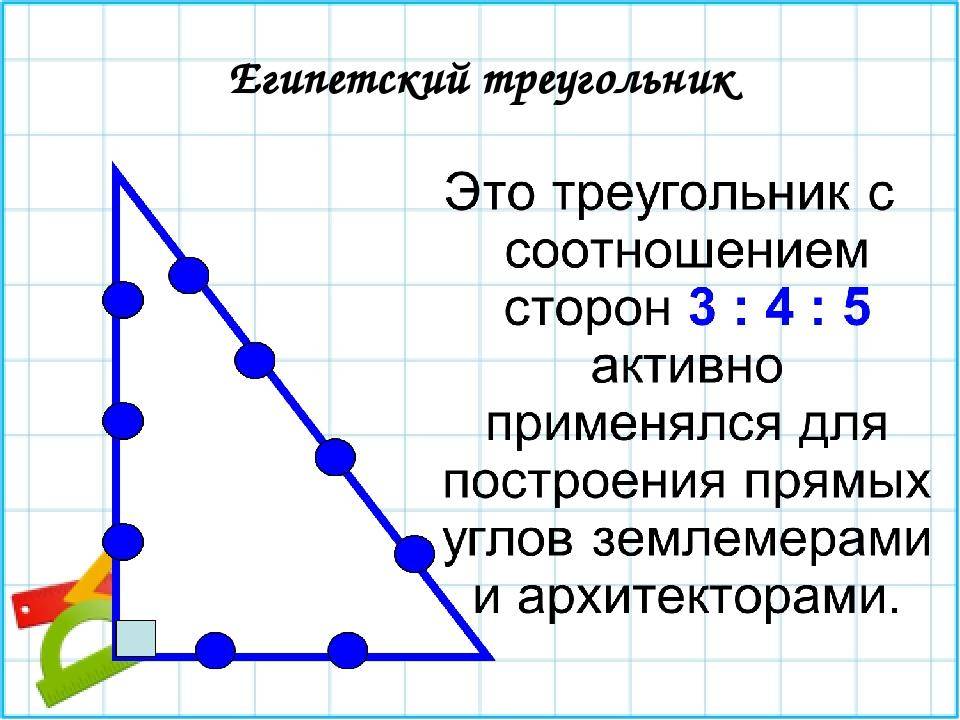
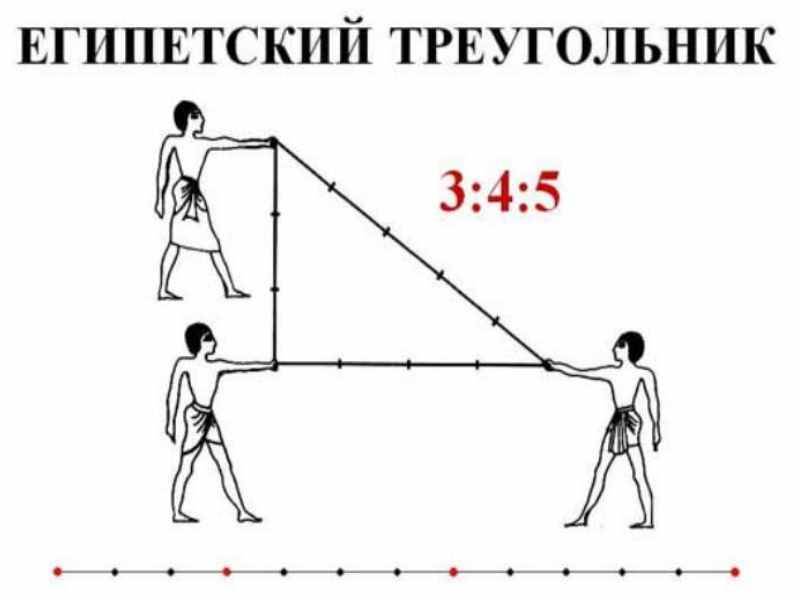
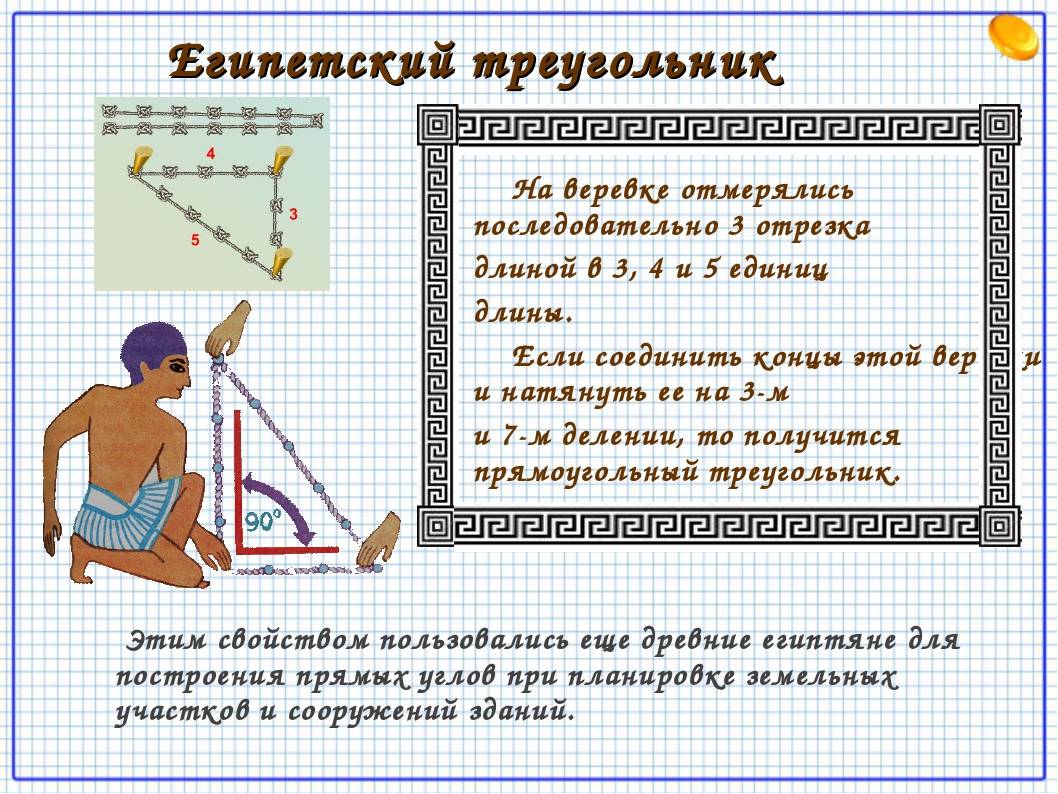
Египетский треугольник в строительстве + свойства

Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

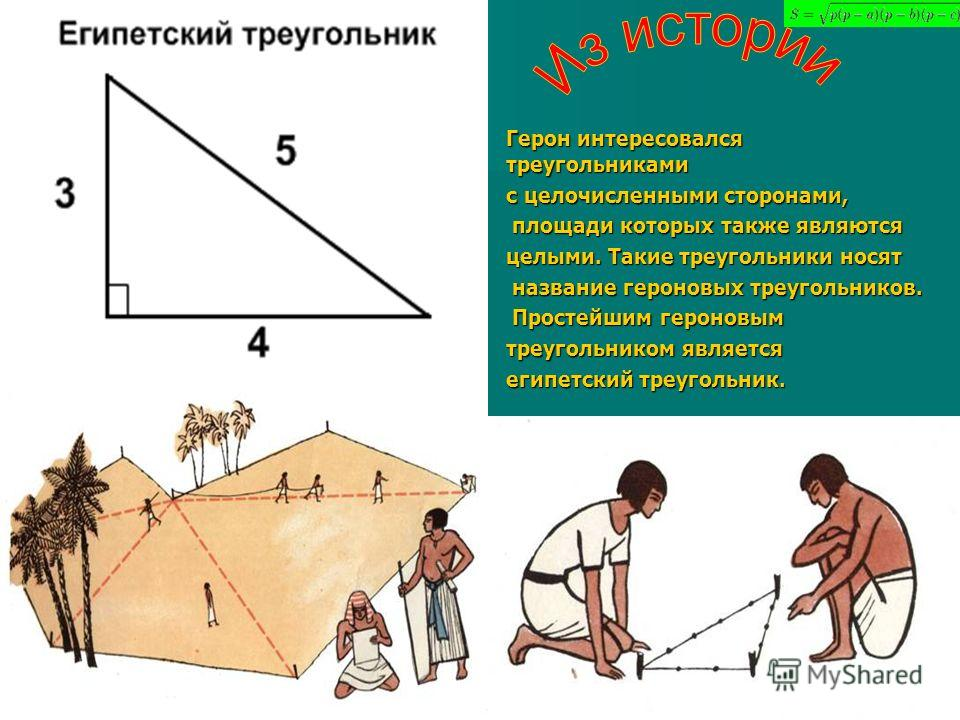
Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

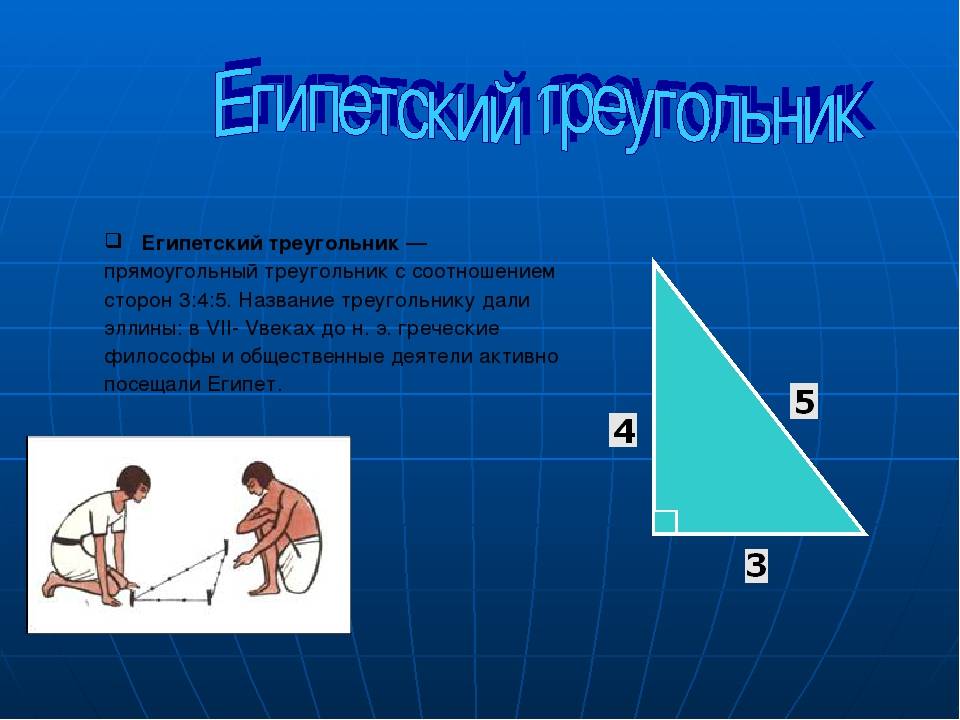
Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.

Строение

Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.

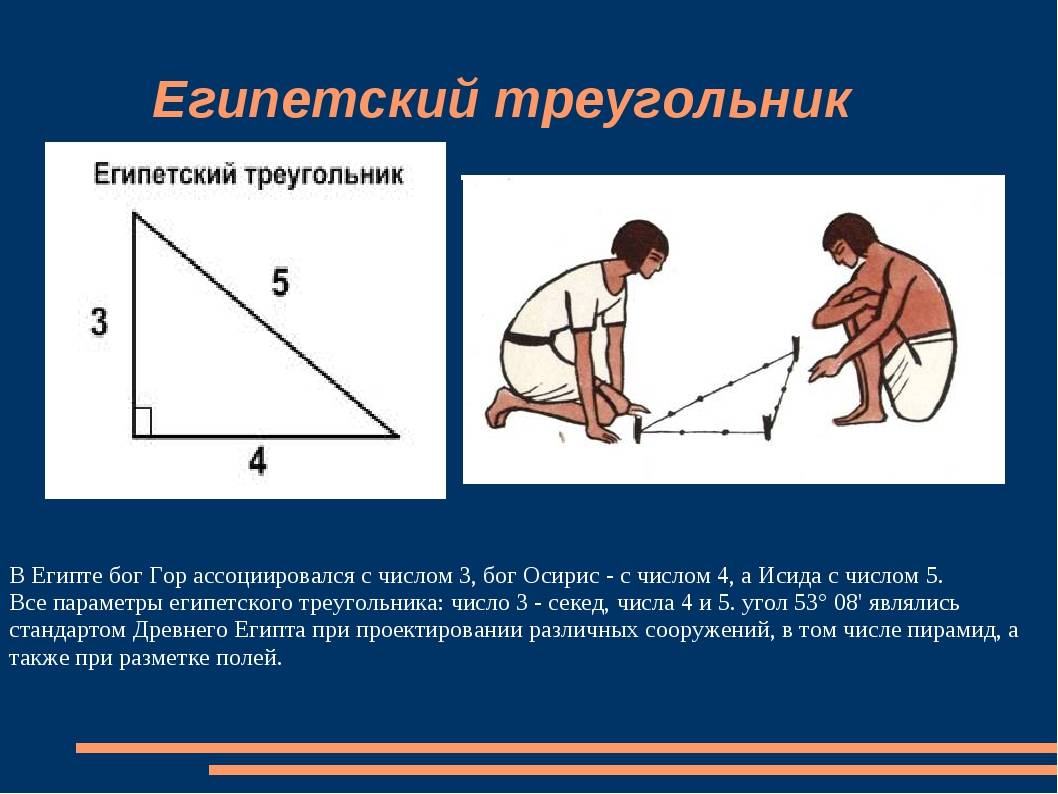
Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.

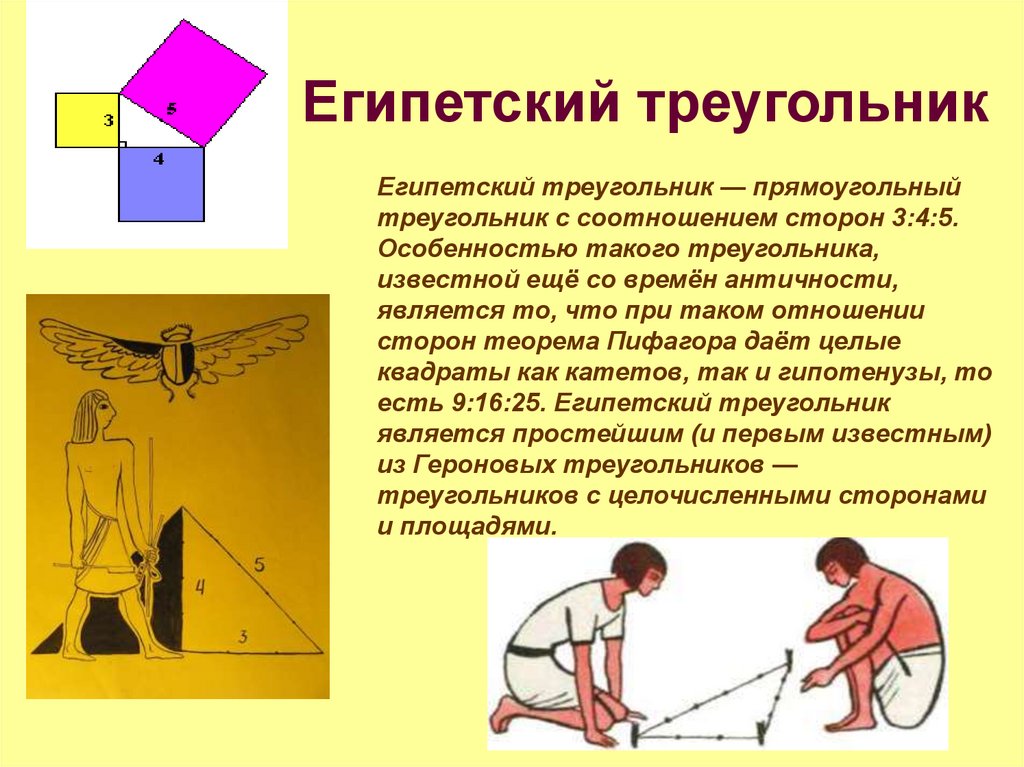
Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?

Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.

Обратное доказательство

Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 32х42=52 и значит он действительно прямоугольный.

Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».

Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.

Особенности

Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:

• все стороны и площадь состоят из целых чисел, как говорилось выше;
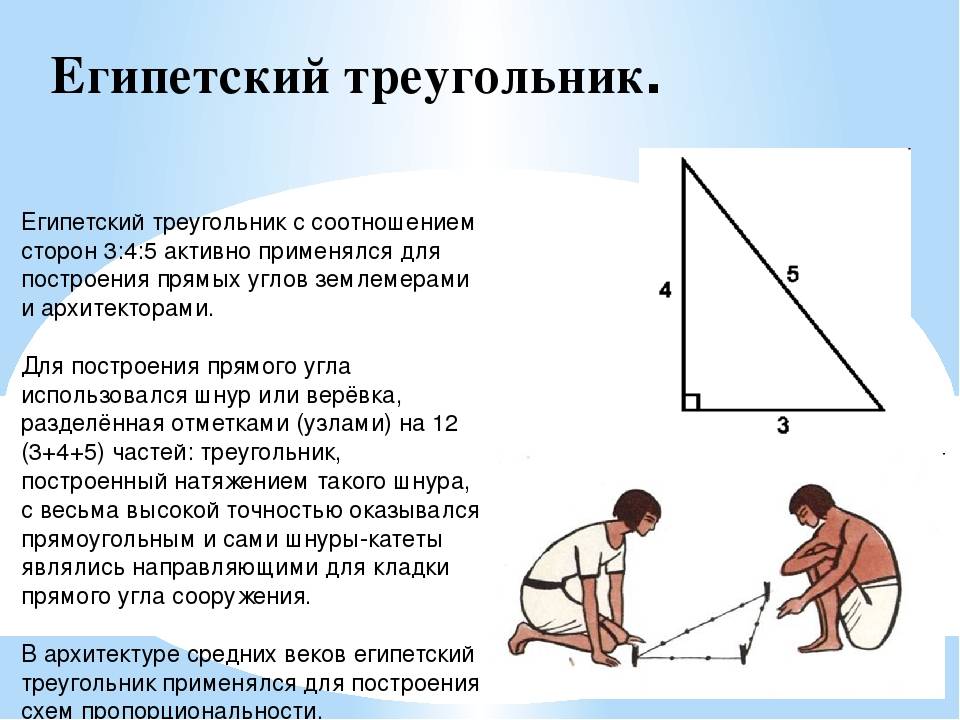
• согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
• такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
• не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.

Кнопки, которые могут отображаться на листе

Рядом с ячейками отображаются семь кнопок: Параметры автозамены

,Параметры вставки , параметры автозаполнения,Ошибка трассировки ,Параметры вставки иприменение правила форматирования .

Параметры автозамены

При наведении указателя мыши на маленькую синюю рамку в разделе текст, который был автоматически исправлен, может появиться кнопка Параметры автозамены

. Например, если ввести в ячейку гиперссылку или адрес электронной почты, может появиться кнопкаПараметры автозамены . Если вы нашли текст, который вы не хотите исправлять, вы можете отменить исправление или включить или отключить параметры автозамены. Чтобы включить или отключить параметры автозамены, нажмите кнопкуПараметры автозамены и выберите нужный вариант из списка.

Угловой

Специальные угловые треугольники, вписанные в единичный круг, удобны для визуализации и запоминания тригонометрических функций, кратных 30 и 45 градусам.

Специальные прямоугольные треугольники «на основе углов» определяются соотношением углов, из которых состоит треугольник. Углы этих треугольников таковы, что больший (прямой) угол, который составляет 90 градусов илиπ2 радиан равен сумме двух других углов.

Длины сторон обычно вычисляются на основе единичной окружности или других геометрических методов. Такой подход можно использовать для быстрого воспроизведения значений тригонометрических функций для углов 30 °, 45 ° и 60 °.

Специальные треугольники используются для помощи в вычислении общих тригонометрических функций, как показано ниже:

градусы	радианы	углы	повороты	грех	потому что	загар	котан
0 °	0 г	√ 2 = 0	√ 42 = 1	неопределенный
30 °	π6	33 +13грамм	112	√ 12 знак равно 12	√ 32	1√ 3	√ 3
45 °	π4	50 г	18	√ 22 знак равно 1√ 2	√ 22 знак равно 1√ 2	1	1
60 °	π3	66 +23грамм	16	√ 32	√ 12 знак равно 12	√ 3	1√ 3
90 °	π2	100 г	14	√ 42 = 1	√ 2 = 0	неопределенный

45 ° –45 ° –90 °

30 ° –60 ° –90 °

Треугольник 45 ° –45 ° –90 °, треугольник 30 ° –60 ° –90 ° и равносторонний / равносторонний (60 ° –60 ° –60 °) треугольник — это три треугольника Мёбиуса на плоскости, что означает, что они разбейте плоскость мозаикой с помощью отражений в их сторонах; см. группу «Треугольник» .

45 ° –45 ° –90 ° треугольник

Установить квадрат

Длины сторон треугольника 45 ° –45 ° –90 °

В плоской геометрии построение диагонали квадрата приводит к треугольнику, три угла которого находятся в соотношении 1: 1: 2, что в сумме дает 180 ° или π радиан. Следовательно, углы составляют соответственно 45 ° (π4), 45 ° (π4) и 90 ° (π2). Стороны этого треугольника находятся в соотношении 1: 1:  √ 2 , что непосредственно следует из теоремы Пифагора .

Из всех прямоугольных треугольников треугольник 45 ° –45 ° –90 ° имеет наименьшее отношение гипотенузы к сумме катетов, а именно √ 22. и наибольшее отношение высоты от гипотенузы к сумме катетов, а именно√ 24.

Треугольники с этими углами — единственные возможные прямоугольные треугольники, которые также являются равнобедренными треугольниками в евклидовой геометрии . Однако в сферической геометрии и гиперболической геометрии существует бесконечно много различных форм прямоугольных равнобедренных треугольников.

Треугольник 30 ° –60 ° –90 °

Установить квадрат

Стороны треугольника 30 ° –60 ° –90 °

Это треугольник, три угла которого находятся в соотношении 1: 2: 3 и составляют соответственно 30 ° (π6), 60 ° (π3) и 90 ° (π2). Стороны находятся в соотношении 1:  √ 3  : 2.

Доказательство этого факта ясно с помощью тригонометрии . Геометрическое доказательство:

Нарисуйте равносторонний треугольник ABC со стороной 2 и точкой D в качестве середины отрезка BC . Нарисуйте линию высоты от A до D . Тогда ABD — это треугольник 30 ° –60 ° –90 ° с гипотенузой длины 2 и основанием BD длины 1.

Тот факт, что оставшаяся катета AD имеет длину √ 3, немедленно следует из теоремы Пифагора .

Треугольник 30 ° –60 ° –90 ° — единственный прямоугольный треугольник, углы которого находятся в арифметической прогрессии. Доказательство этого факта простое и следует из того факта, что если α , α + δ , α + 2 δ — углы в прогрессии, то сумма углов 3 α + 3 δ = 180 °. После деления на 3 угол α + δ должен составлять 60 °. Прямой угол равен 90 °, а оставшийся угол равен 30 °.

Египетский треугольник в строительстве

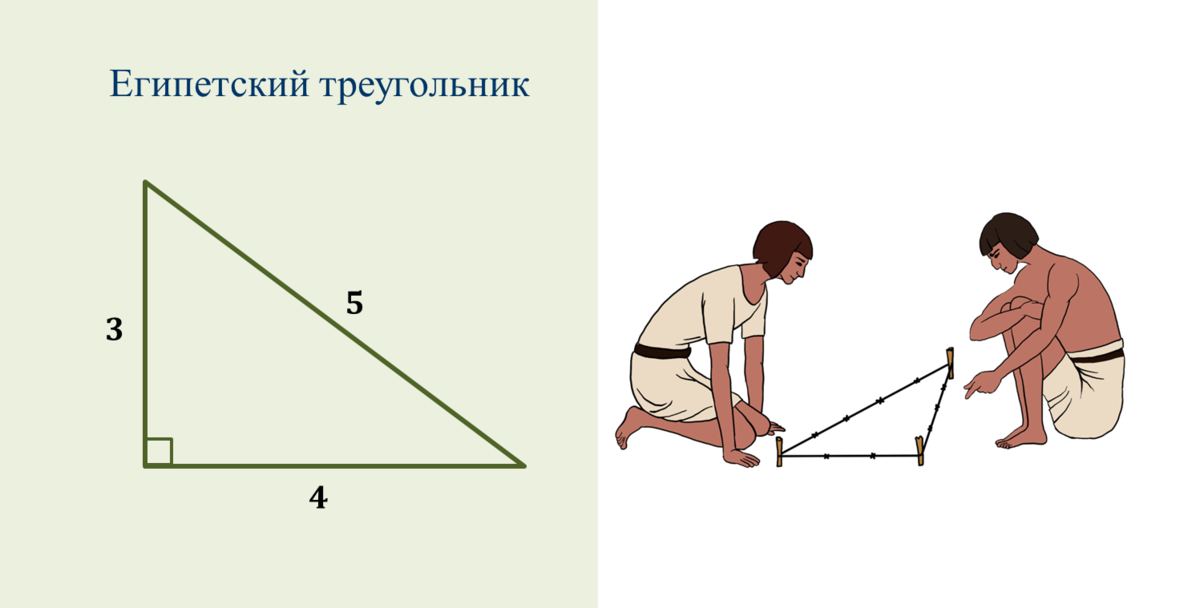
Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника. Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

Стороны конструкции имеют следующее соотношение друг к другу:

Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

1. 5,
2. 4,

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов. Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять

В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять

Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

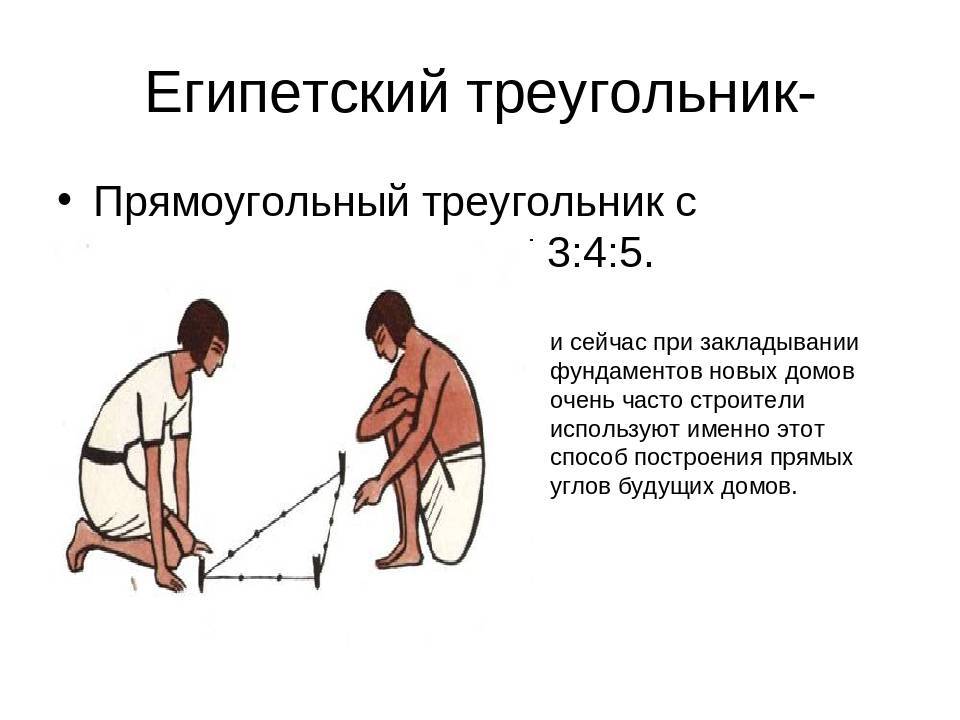
Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

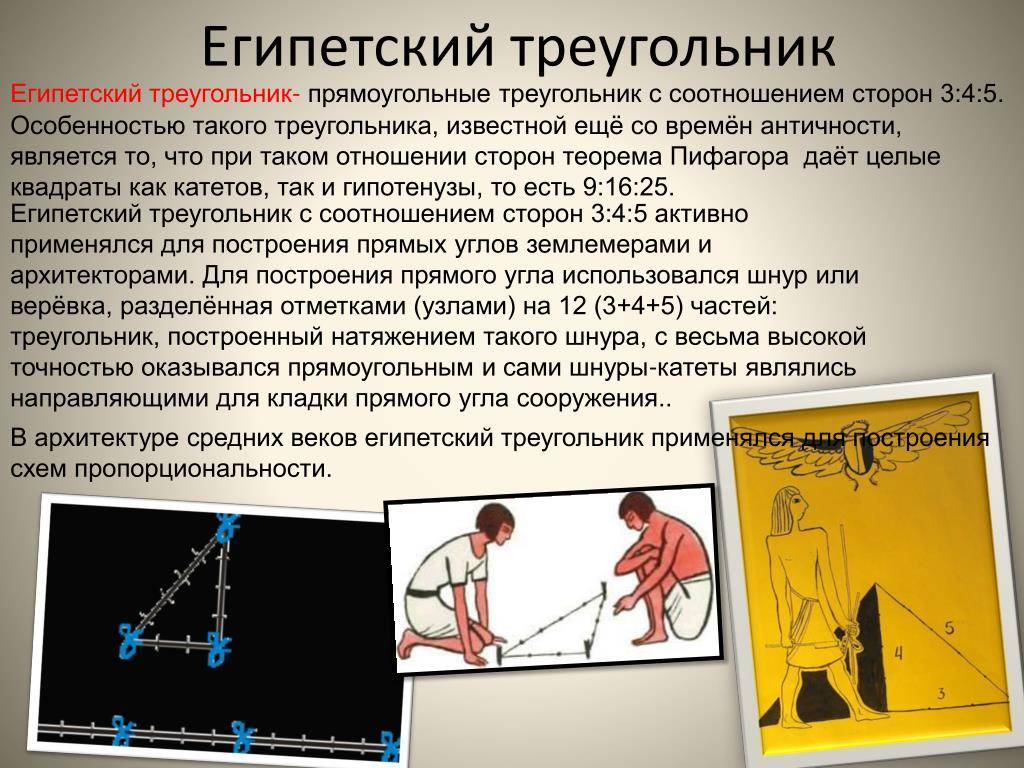
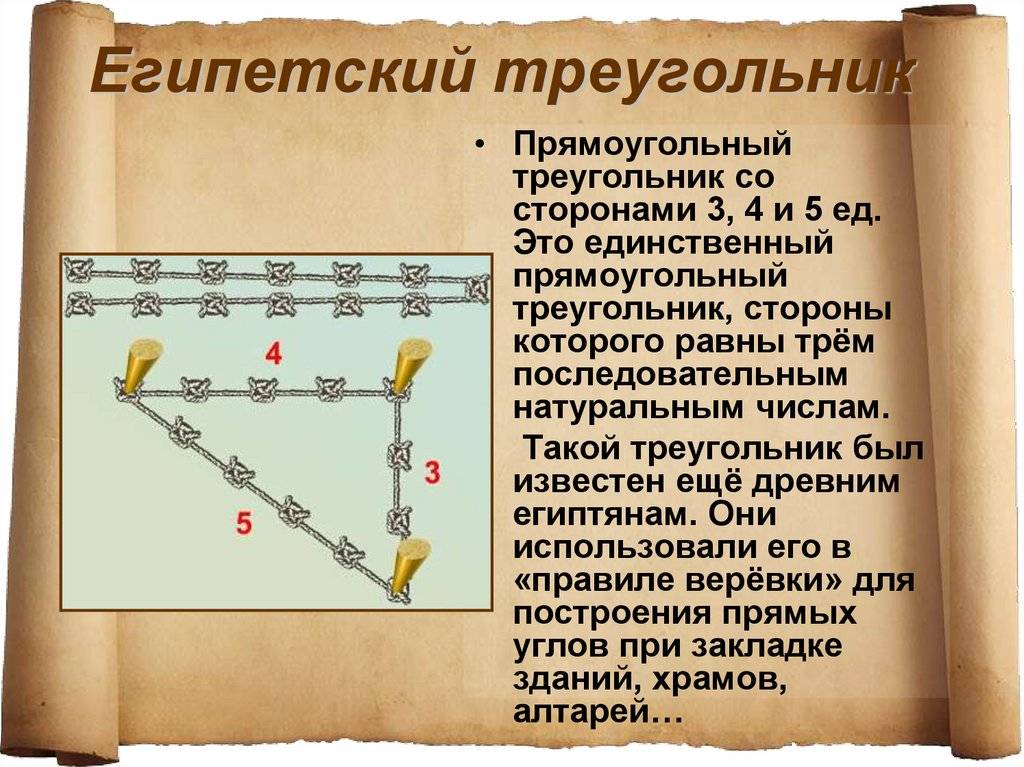
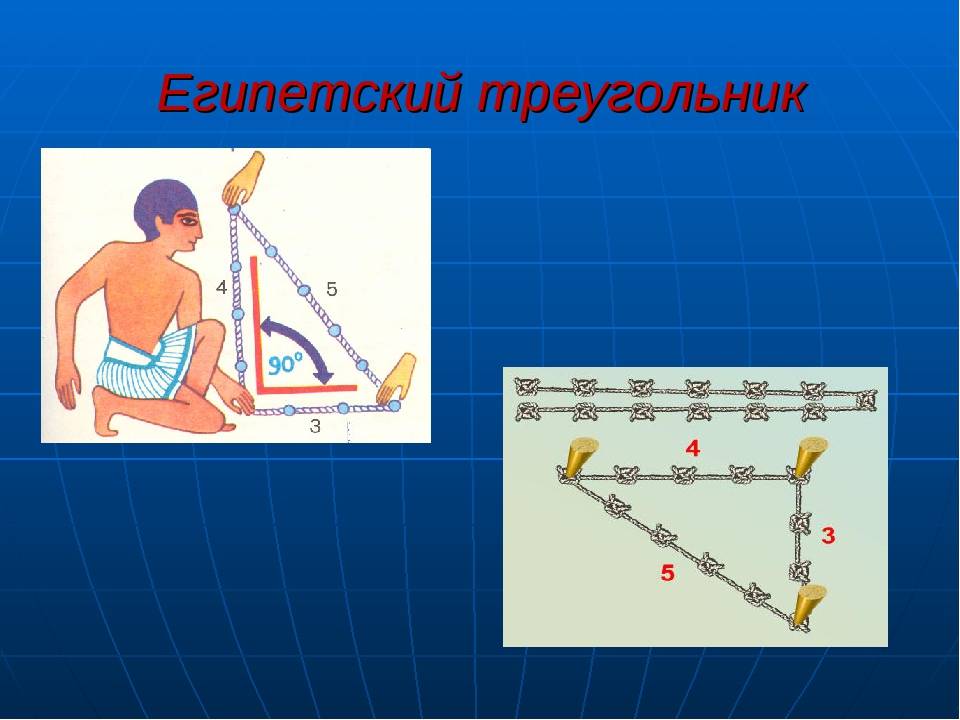
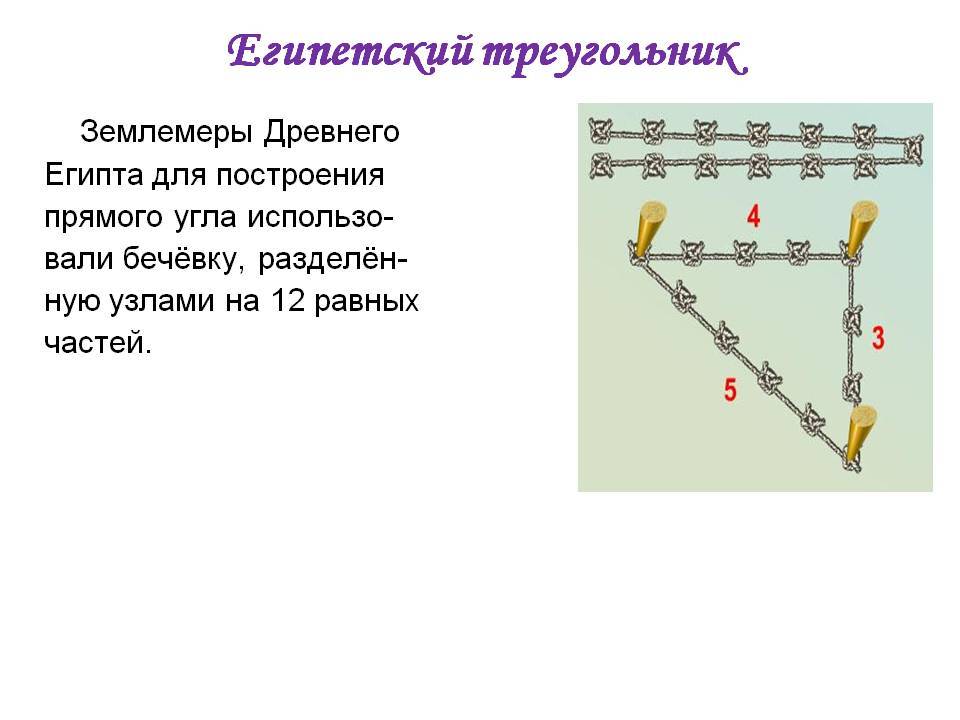
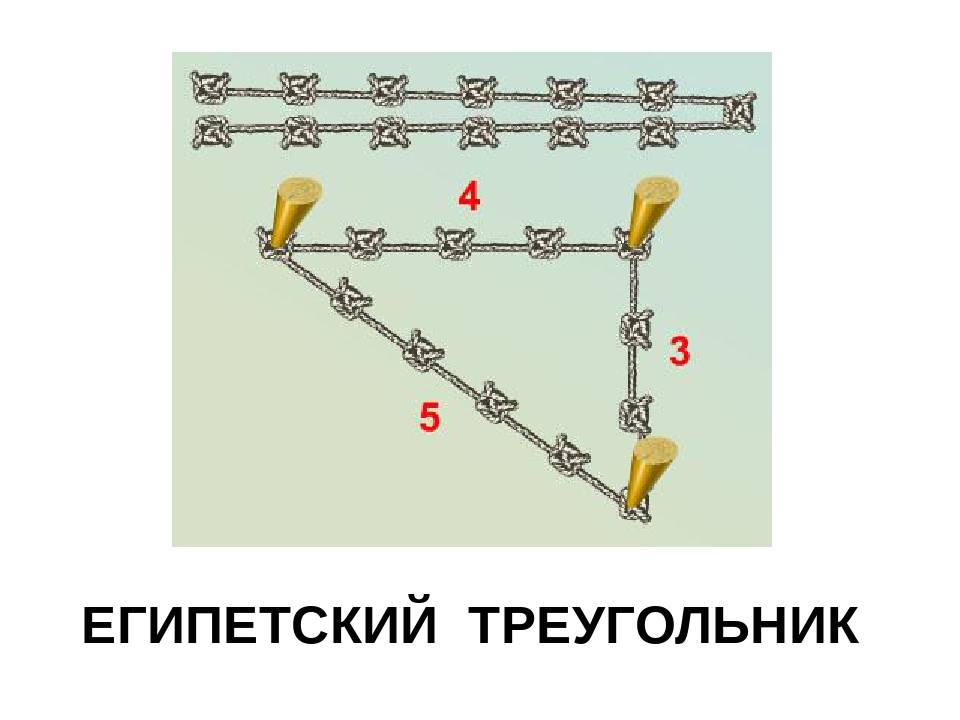
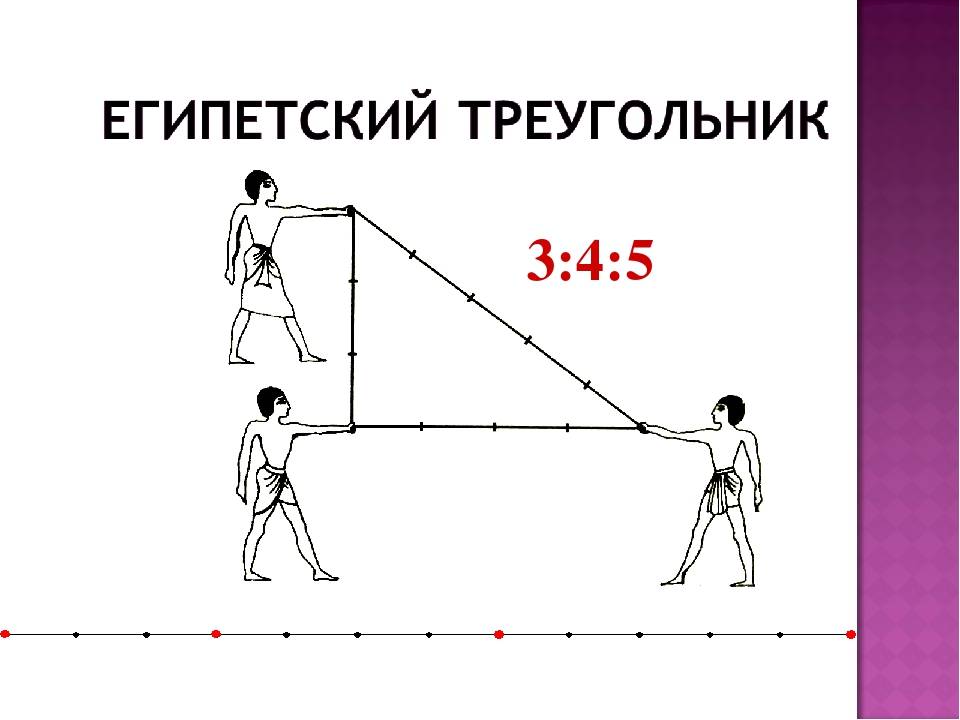
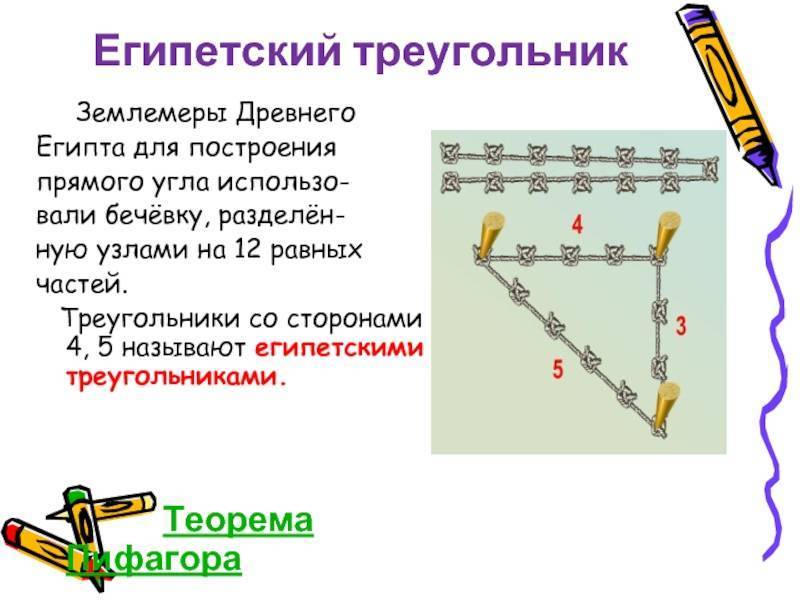
Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол. Края должны совпасть

Края должны совпасть.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках

Глупая ошибка строителей

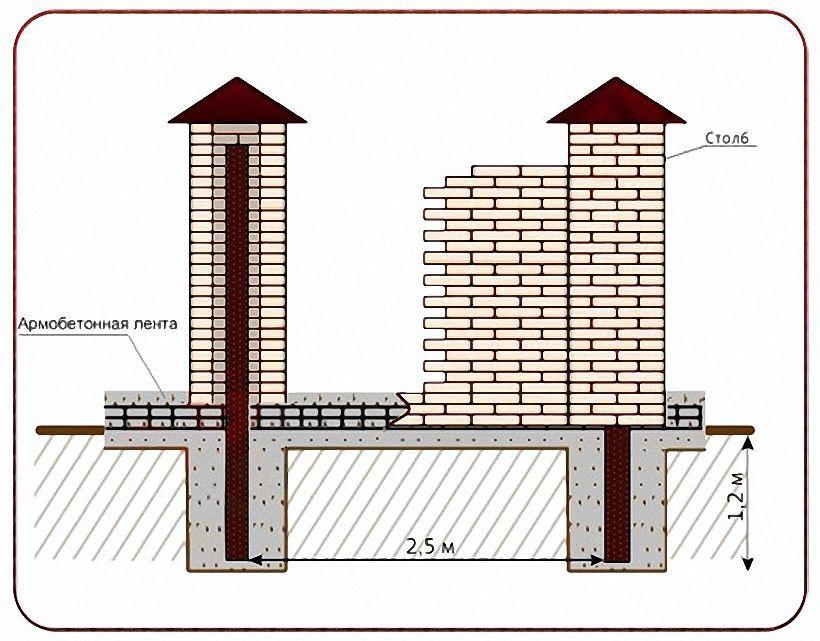
«Египетский треугольник» действительно может помочь в разметке периметра фундамента, однако применение этого метода требует сохранения чётких пропорций. Небольшое отклонение от них − и угол уже не будет прямым. А это приведёт к разнице длин стен. Не единичны случаи, когда при идеальном совпадении длин диагоналей стены получаются разными. Ведь если вдуматься, то трапеция также подходит под заданные параметры, её диагонали равны, в то время как верхняя и нижняя сторона имеют разные длины.

ФОТО: youc.irПравильная трапеция также имеет одинаковые длины диагоналей, однако на квадрат она явно не тянет

Общее значение

В общем значении тату треугольника обозначает гармонию. Каждая из вершин треугольника обозначает какое-то составляющее человеческого характера и сущности. Таким образом, зачастую это – разум, физическое тело и душа человека. Работая совместно, считается, что эти три составляющих дополняют друг друга, создавая внутреннюю гармонию человека и пробуждая в нем энергию.

Еще одним частым значением такой тату может послужить жизненный цикл человека. Все просто: вершины треугольника – это этапы жизни, то есть рождение, непосредственно жизнь и смерть. Смысл такой тату в том, что, следуя линиям треугольника, вы все равно приходите к первому этапу жизни – к рождению. Это означает то, что жизнь никогда не останавливается, и когда кто-то умирает, вместо него рождается кто-то другой, и так до бесконечности.

В наше время татуировки делаются еще в качестве увековечивания своей любви к другому человеку. Таким образом, делаются также и парные эскизы треугольников для влюбленной пары, которая уверена в своих чувствах.

С точки зрения психологии, треугольник – это наколка, обозначающая лидерство человека. Человек с такой наколкой никогда не терпит поражений, он точен во всем, что, собственно, может понять из самой татуировки.

Еще одно толкование – благосостояние семьи. Все довольно просто и не требует особых объяснений, поскольку можно четко вывести то, что каждая вершина – мать, отец и дети.

Что такое угольник и для чего он предназначен

Угольником называется измерительный инструмент, состоящий из двух линеек, расположенных под углом 90 градусов друг к другу. Применяется он в различных сферах — в строительстве, в слесарном и столярном деле, на производстве и т.п. Главное предназначение этого устройства заключается в нанесении прямых линий, расположенных перпендикулярно друг к другу.

Угольник еще называют поверочным, так как с его помощью осуществляется проверка конструкций на наличие брака. Многие используют этот инструмент только для начертания прямых линий под углом 90 градусов, и даже не догадываются о том, что прибором также можно начертить линию с любым другим наклоном.

Главное достоинство рассматриваемого инструмента в том, что он имеет простую конструкцию. Это отражается не только на его стоимости, но и возможности изготовления своими руками. Чтобы сделать угольник, понадобится соединить две линейки, расположив их перпендикулярно друг к другу. Посредством полученного устройства можно наносить не только перпендикулярные линии, но и параллельные.

Это интересно!Угольник — это главный инструмент плотников, строителей и каменщиков, так как с его помощью осуществляется быстрое и точное измерение прямого угла.

Иные способы выведения прямого угла

Если нет желания заниматься выведением углов самостоятельно, а финансы позволяют обратиться за помощью к специалистам, можно вообще не думать об этом вопросе. Один звонок − и на участке уже находится геодезист с теоделитом, который в сжатые сроки сделает разметку. Однако в этом случае необходимо быть готовым к внушительным затратам на оплату его труда.

ФОТО: omegagalvanoplastia.com.brТеоделит – высокоточная техника, однако стоимость подобной разметки может влететь «в копеечку»

Если говорить о минимальных затратах, то, основываясь на прайс-листах фирм, оказывающих подобные услуги, вызов и работа геодезиста с инструментом обойдётся в 1 000 руб./час при минимальной оплате 7 000 руб. Дальше − больше. Разметка осей (2 точки) – ещё 3 000 рублей. Если же потребуется определить точные координаты по GPS, то здесь каждые три точки обойдутся владельцу в 5 000 руб. Можно посчитать, какова будет общая сумма (все цены указаны с учётом на конец сентября 2020 года). Не проще ли самому произвести все необходимые разметки? Ведь сэкономленные средства всегда можно потратить на что-то полезное в дальнейшем строительстве.

ФОТО: thelundreport.orgСтоит приготовиться к тому, что карман значительно облегчится

Как добраться?

Быстрее всего добраться к Египетскому мосту в Санкт-Петербурге можно от станции метро «Балтийская». Нужно выйти на этой станции и проследовать на Обводный канал. Оттуда свернуть на Лермонтовский проспект, по которому нужно пройти еще минут 10-15. Вдали появятся очертания известных зеленых обелисков под светом фонарей, и там же – фигуры сфинксов, охраняющих вход на мост.

Если есть немного свободного времени и желания пройтись, также можно выйти на станции «Технологический Институт», оттуда перейти на 1-ю Красноармейскую, а затем свернуть на проспект Троицкий. Так можно будет по дороге посмотреть Троицкий собор Санкт-Петербурга.

Адрес: г. Санкт-Петербург, Набережная реки Фонтанки, 151-153.

Watch this video on YouTube

Разметка под фундамент своими руками

Качество постройки в огромной степени зависит от того, насколько правильно была выполнена разметка под фундамент

Занимаясь этой работой важно с максимальной точностью выдержать все прямые углы. Разметка фундамента своими руками под частный дом может быть выполнена несколькими способами. Чаще всего используются метод «египетского» треугольника и метод двух кривых

Поэтому в этой статье рассмотрим именно их

Чаще всего используются метод «египетского» треугольника и метод двух кривых. Поэтому в этой статье рассмотрим именно их.

Какие инструменты понадобятся?

Производится разметка фундамента своими руками с применением инструментов:

• Рулетки;
• Шнура;
• Гидроуровня и отвеса;
• Помимо этого понадобятся деревянные колышки.

С чего начать разметку?

Итак, как провести разметку фундамента? Для начала следует определить две исходные точки, вбив колышки по углам будущего здания, находящимся на одной прямой со стороны его самой длинной стены. Далее от них нужно будет провести перпендикуляры, таким образом отметив внешний контур смежных стен.

«Египетский треугольник». Самый простой метод

Разметка фундамента своими руками быстрее всего может быть произведена методом «золотого» треугольника, имеющего соотношение длин сторон 5*3*4. Мероприятие при этом выполняется в несколько этапов:

1. Для начала нужно найти длинную веревку и завязать на ней четыре узла. Первый – на конце, второй на расстоянии 3м, третий в четырех метрах от второго и последний в пяти метрах от третьего; 2. После этого самый первый и самый последний узлы соединяют гвоздем. По гвоздю следует вбить и в каждый из промежуточных узлов; 3. При этом длинную сторону получившегося треугольника нужно расположить вдоль линии между двумя уже вбитыми колышками; 4. Вдоль короткой стороны проводят требуемый перпендикуляр; 5. На полученной прямой, вбивают третий колышек на расстоянии равном ширине здания.

Важно: Правильность всех замеров следует обязательно проверить. Для этого между вбитыми кольями по диагоналям натягивают два шнура и связывают в месте пересечения

Paste a VALID AdSense code in Ads Elite Plugin options before activating it.

Метод двух дуг

Разметка фундамента своими силами этим методом выполняется также с использованием веревки. Предварительно от одного из колышков в обе стороны по уже имеющейся прямой отмеряют равные расстояния и отмечают найденные места. Далее к одной из полученных точек прикрепляют веревку с привязанным на противоположном конце гвоздем. Натянув ее проводят дугу напротив того колышка, от которого отмерялись расстояния. Затем веревку крепят ко второму отмеченному месту и чертят еще одну дугу. Из той точки, где дуги пересекутся, проводят линию к колышку. В результате получается прямой угол между ней и уже имеющейся линией.

На заключительном этапе к кольям на высоте будущего фундамента привязывают шнур, поверяя горизонтальность его положения со всех четырех сторон, пользуясь строительным уровнем. Для ленточного фундамента чертят внутренний контур параллельно найденному внешнему и также натягивают шнур.

Совет: В том случае, если траншею предполагается копать с привлечением техники, шнуры лучше не использовать. В процессе работы они могут порваться. Линии между найденными точками в этом случае стоит прочертить песком. Для нахождения центров столбов столбчатого фундамента, от найденных углов вдоль прочерченных линий отмеряют необходимые расстояния и ставят отметки. Далее проверяют прямоугольность углов, получившихся на пересечении линий (соединяющей полученные точки на противоположных сторонах и линии периметра, на которой расположены отметки).

Разметка фундамента своими руками, как можно было заметить – процедура не такая уж и сложная. Самое главное, делать все аккуратно, хорошо натягивать веревку и обязательно проверять полученный результат методом диагоналей.

2а. ПРАВИЛА ПРИЕМКИ

2а.1. Для проверки соответствия угольников требованиям настоящего стандарта предприятие-изготовитель должно проводить приемочный контроль, периодические испытания и испытания на надежность.

(Измененная редакция, Изм. № 3).

2а.2. При приемочном контроле каждый угольник проверяют на соответствие требованиям пп. 2.1- 2.7, 2.9- 2.11.

2а.3. Периодические испытания проводят не реже раза в три года. Периодическим испытаниям подвергают не менее трех угольников, из числа прошедших приемочный контроль, на соответствие всем требованиям настоящего стандарта.

При этом показатели п. 2.17 подтверждаются результатами анализа подконтрольной эксплуатации не менее пяти угольников. Результаты анализа подконтрольной эксплуатации считают положительными, если: среднее значение полного срока службы контролируемых угольников не менее 5 лет ( п. 2.17), все контролируемые угольники не достигнут предельного состояния в течение 2,5 лет ( п. 2.17).

Если при испытаниях обнаружено, что угольники соответствуют всем требованиям настоящего стандарта, результаты периодических испытаний считают удовлетворительными.

(Измененная редакция, Изм. № 3, 4).

Конструкция

Новая переправа не была создана по подобию старого. Основной целью нового Египетского моста в Питере было соединить два берега реки Фонтанки, при этом оставаясь легкой и не затратной конструкцией. Но совсем отойти от применения мотивов Древнего Египта новые архитекторы не решились.

В дизайне использовались украшения лавровыми венками и цветами лотоса. Также сохранились сфинксы, что и позволило оставить прежнее название.

Последнюю реконструкцию чугунных сфинксов провели в 2004 году, обнаружив первоначальный слой позолоты на их головах. Скульптуры были сильно повреждены, во многих местах имелись трещины. Все отпечатки времени удалили, скульптуры снова позолотили. На сегодня сфинксы относятся к старейшим памяткам культуры Санкт-Петербурга.

Начинаем разметку от первой стены

Первым делом проверим нашу первую стену на вертикаль и плоскость. Если выравниваем 2 угла, то это стена, параллельная ванне, если выравниваем 4 угла (всю площадь), то стена с проёмом. Если стена завалена, её нужно будет выровнять первым делом, но не торопитесь, ведь мы ещё не проверили всю площадь.

Для начала просто отобьём ровную линию параллельно первой стене, максимально приближённую к ней.

Проведём первую линию, параллельно первой стены

Далее между первой стеной и второй стеной установим угольник одной гранью параллельно первой линии, а на вторую грань угольника накладываем прави́ло. Совмещаем грань прави́ла и угольника, тем самым «удлинняя» наш угольник. Чертим линию на полу до конца стены максимально приближённую к стене. Регулируем и совмещаем наш увеличенный угольник так что бы:

• линия была ровной,
• расстояние до стены минимальным,
• вторая грань угольника была параллельна первой линии.

Так получаем первый прямой угол.

От первой линии отобьём вторую, перпендикулярную ей

Далее идём на следующий угол, до которого мы чертили линию, и совмещаем угольник одной гранью параллельно второй линии. Повторяем процедуру с правилом (совмещаем его с угольником) и чертим третью линию перпендикулярную второй, опять же максимально приближённую к стене.

Тут требуется некоторая сноровка, чтобы совмещать прави́ло, угольник и делать прямой угол с линиями, максимально приближёнными к стене (это делается для того, что бы при штукатурке «не съесть» лишнее пространство). Если прави́ла не хватает, дочерчиваем до куда хватает, переставляем прави́ло, совмещая его с линией, и проводим её до конца стены.

Чертим третью линию перпендикулярную второй

Чертим четвёртую линию, по аналогии. В итоге у нас должен получится начерченный на полу прямоугольник

внутри нашего помещения. Проверяем его по первой грани — по стене с проёмом, так же, прикладывая угольник и правило.

Проверяем по 1-й грани полученный прямоугольник

Если всё ровно, можно немного расслабиться. Если нет, повторяем процедуру и/или смотрим где ошиблись.

Заключительное слово

Что бы ни говорили противники описанного метода измерений, но «египетский треугольник» в значительной степени помогает строителям в выведении прямых углов. Конечно, при условии его правильного использования. Тем более что навязать 12 узлов на верёвке на определённом расстоянии один от другого много времени не потребует. Также это не потребует и финансовых затрат, связанных с наймом геодезиста с необходимым оборудованием.

ФОТО: profipol.dp.uaТак должны быть расположены узлы на верёвке для построения «египетского треугольника»

Watch this video on YouTube

Предыдущая DIY HomiusПрочные хомуты из ПЭТ-бутылки за минуту
Следующая DIY HomiusСмеяться или плакать: ошибки во время ремонта

Почти равносторонние треугольники Герона

Поскольку площадь равностороннего треугольника с рациональными сторонами является иррациональным числом , ни один равносторонний треугольник не является героновым. Однако существует уникальная последовательность треугольников Герона, которые являются «почти равносторонними», поскольку три стороны имеют форму n  — 1, n , n  + 1. Метод генерации всех решений этой задачи на основе цепных дробей описан в 1864 г. Эдвард Санг , а в 1880 г. Рейнхольд Хоппе дал замкнутое выражение для решений. Первые несколько примеров этих почти равносторонних треугольников перечислены в следующей таблице (последовательность A003500 в OEIS ):

Длина стороны	Площадь	Inradius
п — 1	п	п + 1
3	4	5	6	1
13	14	15	84	4
51	52	53	1170	15
193	194	195	16296	56
723	724	725	226974	209
2701	2702	2703	3161340	780
10083	10084	10085	44031786	2911
37633	37634	37635	613283664	10864

Последующие значения n можно найти, умножив предыдущее значение на 4, а затем вычтя предыдущее значение (52 = 4 × 14 — 4, 194 = 4 × 52 — 14 и т. Д.), Таким образом:

птзнак равно4пт-1-пт-2,{\ Displaystyle п_ {т} = 4n_ {т-1} -n_ {т-2} \ ,,}

где t обозначает любую строку в таблице. Это последовательность Лукаса . В качестве альтернативы формула генерирует все n . Аналогично, пусть A = площадь и y = радиус, тогда
(2+3)т+(2-3)т{\ displaystyle (2 + {\ sqrt {3}}) ^ {t} + (2 — {\ sqrt {3}}) ^ {t}}

((п-1)2+п2+(п+1)2)2-2((п-1)4+п4+(п+1)4)знак равно(6пу)2знак равно(4А)2{\ displaystyle {\ big (} (n-1) ^ {2} + n ^ {2} + (n + 1) ^ {2} {\ big)} ^ {2} -2 {\ big (} ( n-1) ^ {4} + n ^ {4} + (n + 1) ^ {4} {\ big)} = (6ny) ^ {2} = (4A) ^ {2}}

где { n , y } — решения n 2  — 12 y 2  = 4. Небольшое преобразование n = 2x дает обычное уравнение Пелла x 2  — 3 y 2  = 1, решения которого затем могут быть получены из регулярного продолжения дробное разложение для √ 3 .

Переменная n имеет вид , где k равно 7, 97, 1351, 18817,…. Числа в этой последовательности обладают тем свойством, что k последовательных целых чисел имеют целое стандартное отклонение .
пзнак равно2+2k{\ displaystyle n = {\ sqrt {2 + 2k}}}