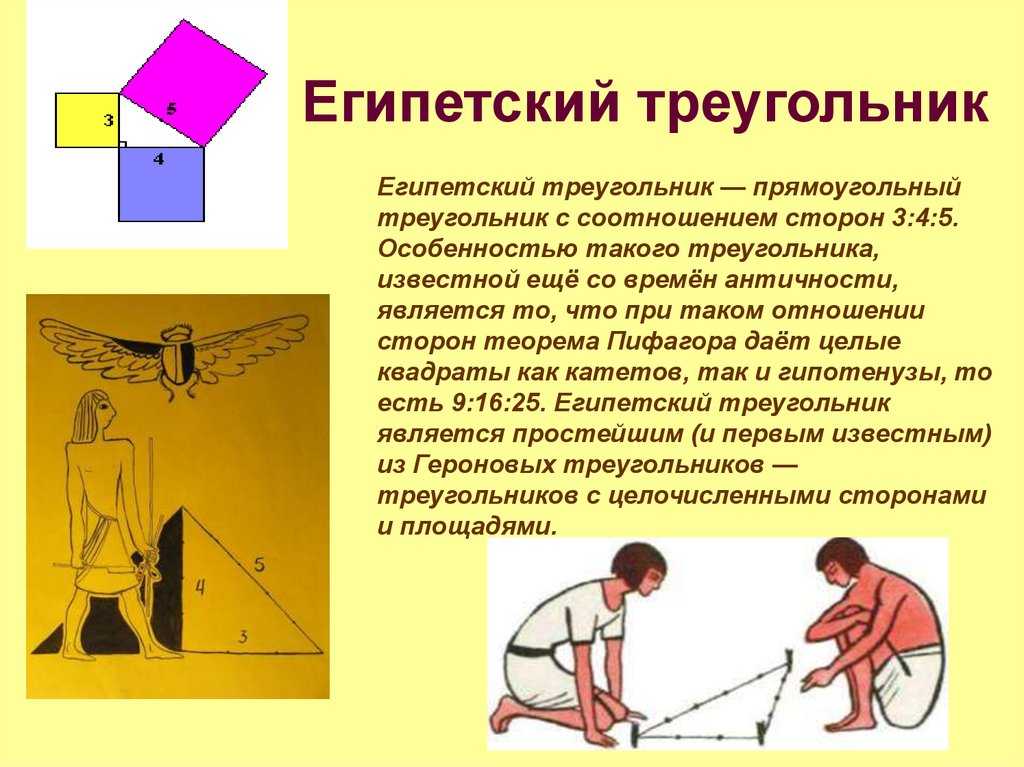
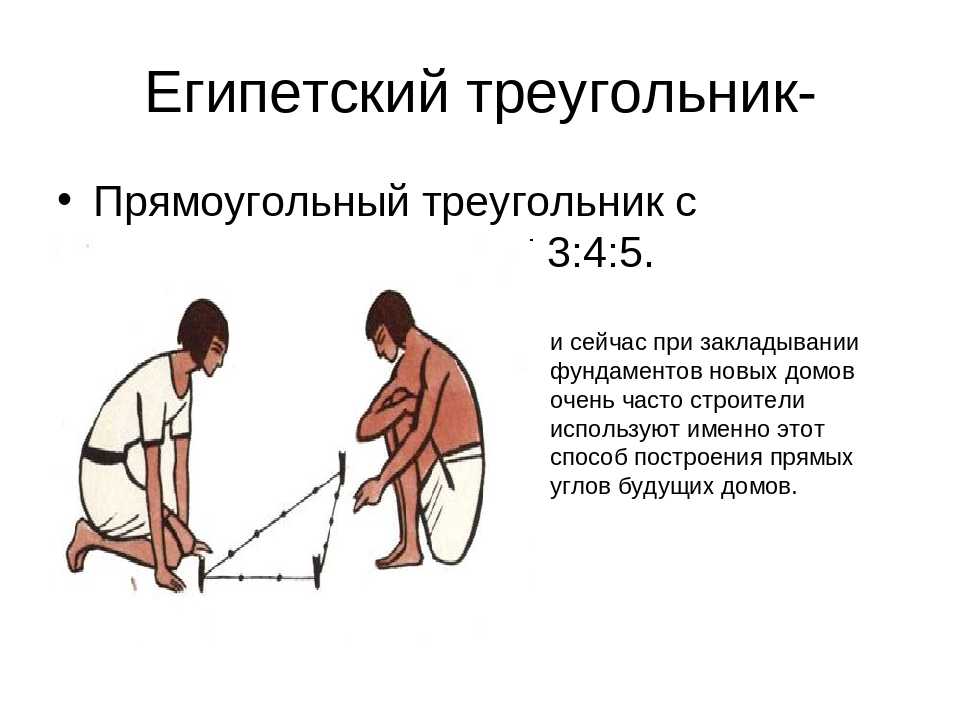
Египетский треугольник
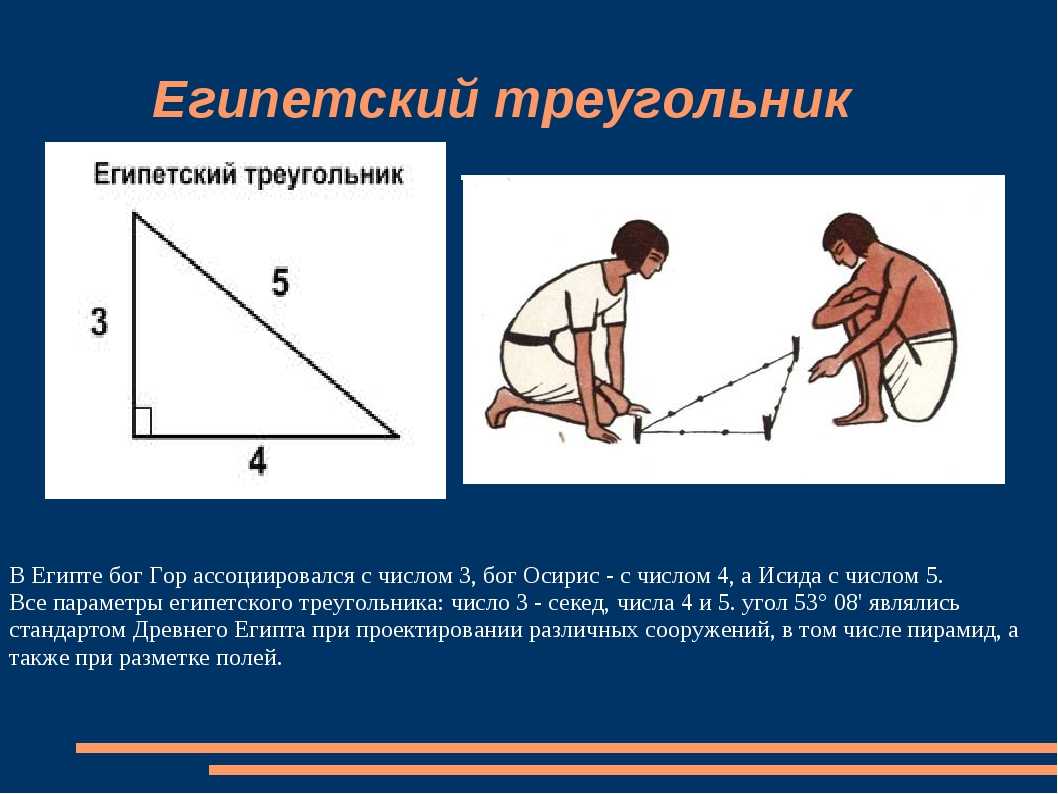
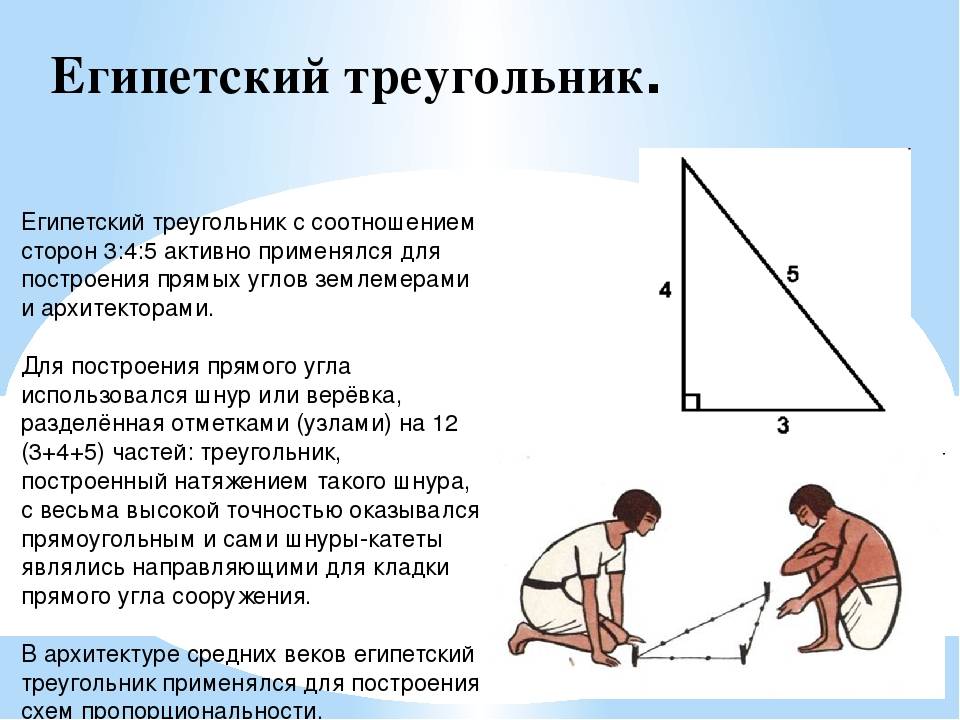
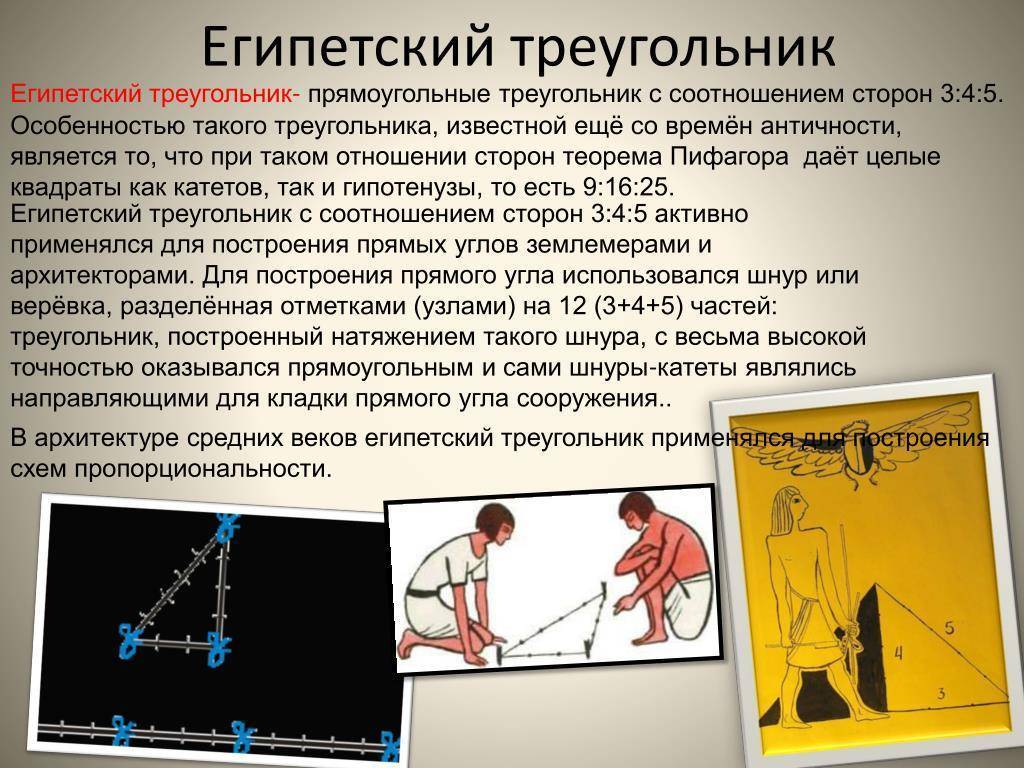
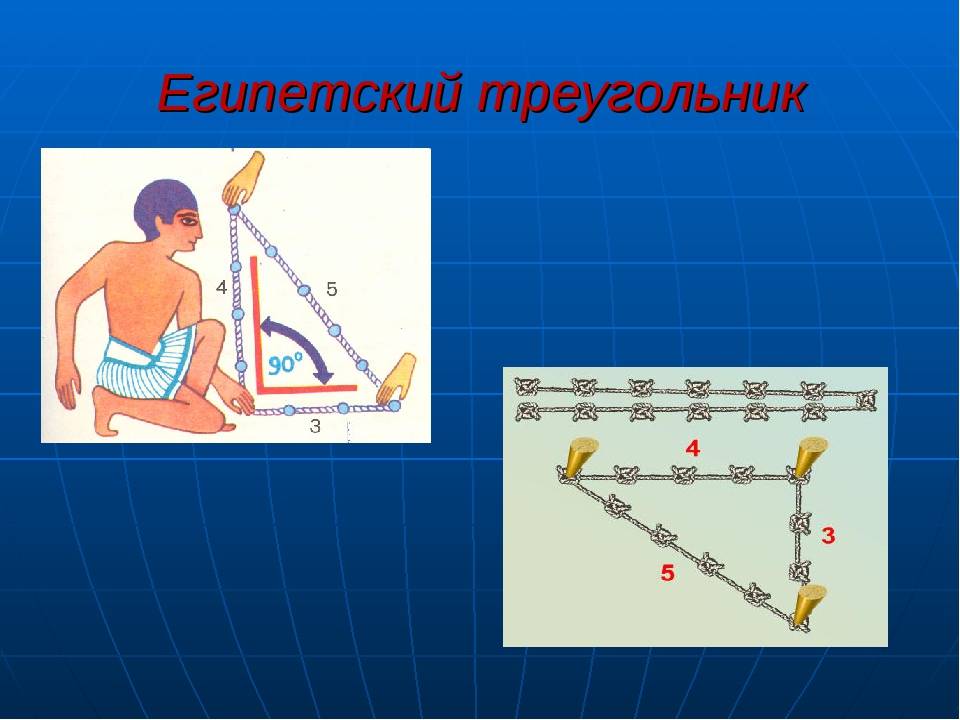
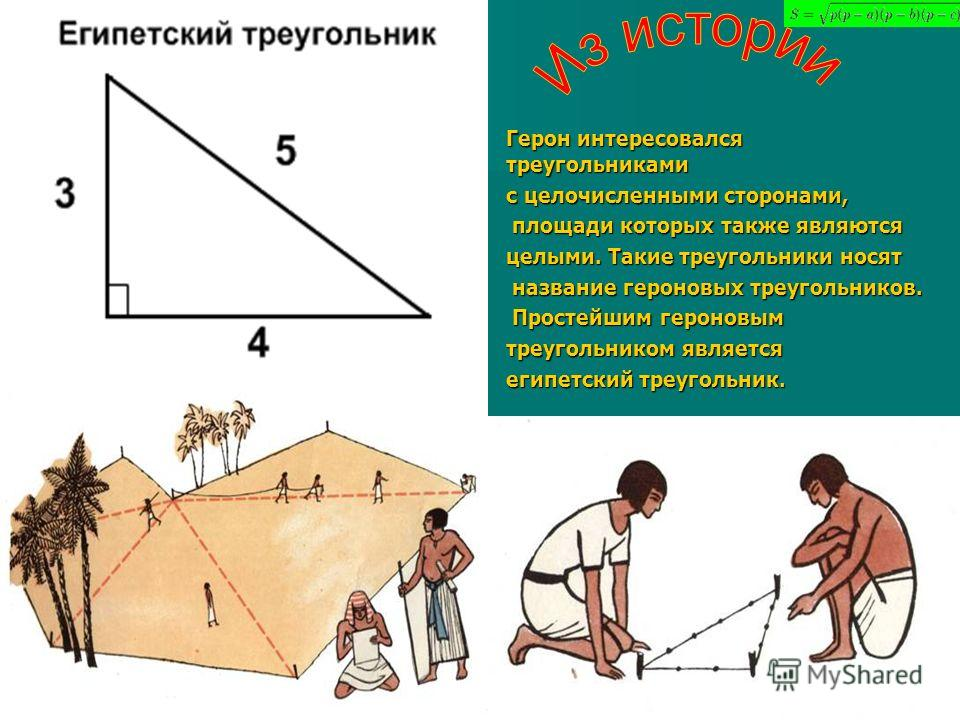
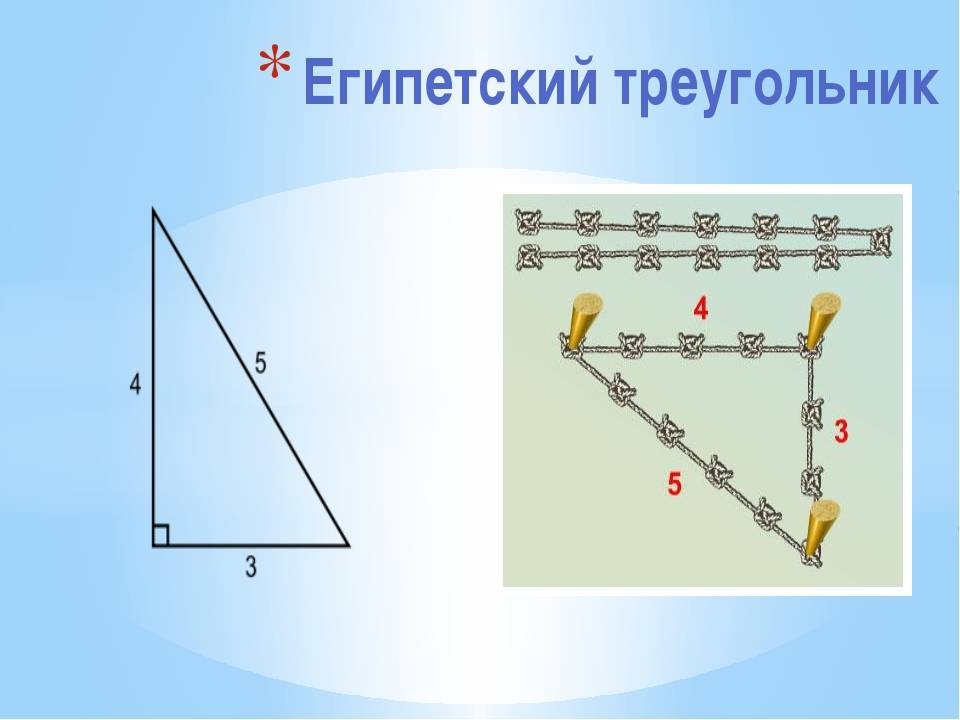
Египетский треугольник – прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся египетский треугольник в архитектуре средних веков для построения схем пропорциональности.
Итак, с чего же начать? Разве вот с этого: 3 + 5 = 8. а число 4 составляет половину числа 8. Стоп! Числа 3, 5, 8… Разве они не напоминают что-то очень знакомое? Ну конечно, они имеют прямое отношение к золотому сечению и входят в так называемый «золотой ряд»: 1, 1, 2, 3, 5, 8, 13, 21… В этом ряду каждый последующий член равен сумме двух предыдущих: 1 + 1= 2. 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8 и так далее. Выходит, что египетский треугольник имеет отношение к золотому сечению? И древние египтяне знали, с чем имели дело? Но не будем торопиться с выводами. Необходимо выяснить детали поточнее.
Выражение «золотое сечение», как считают некоторые, впервые ввел в XV веке Леонардо да Винчи. Но сам «золотой ряд» стал известен в 1202 году, когда его впервые опубликовал в своей «Книге о счете» итальянский математик Леонардо Пизанский. Прозванный Фибоначчи. Однако почти за две тысячи лет до них золотое сечение было известно Пифагору и его ученикам. Правда, называлось оно по-другому, как «деление в среднем и крайнем отношении». А вот египетский треугольник с его «золотым сечением» был известен еще в те далекие времена, когда строились пирамиды в Египте, когда процветала Атлантида.
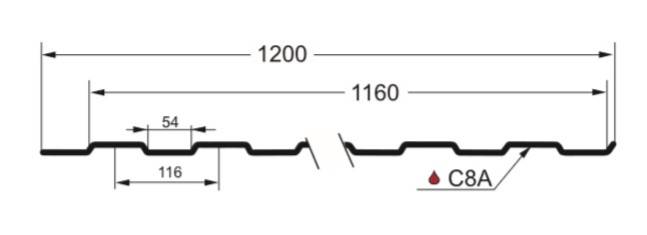
Для доказательства теоремы о египетском треугольнике необходимо использовать отрезок прямой известной длины А-А1 (рис.). Он будет служить масштабом, единицей измерения, и позволит определить длину всех сторон треугольника. Три отрезка А-А1 равны по длине наименьшей из сторон треугольника ВС, у которой соотношение равно 3. А четыре отрезка А-А1 равны по длине второй стороне, у которой соотношение выражается числом 4. И, наконец, длина третьей стороны равна пяти отрезкам А-А1. А дальше, как говорится, дело техники. На бумаге проведем отрезок ВС, являющийся наименьшей стороной треугольника. Затем из точки В радиусом, равным отрезку с соотношением 5, проводим циркулем дугу окружности, а из точки С —дугу окружности радиусом, равным длине отрезка с соотношением 4. Если теперь точку пересечения дуг соединить линиями с точками В и С, то получим прямоугольный треугольнике соотношением сторон 3 : 4 : 5.
Что и требовалось доказать.
Египетские пирамиды строили инопланетяне?
Наверное внеземное вмешательство – это первое что приходит в голову, когда видишь пирамиды в живую. И действительно, в сознании не укладывается, что такое могли построить люди 4500 лет назад без современных технологий. Однако, других веских доказательств инопланетного вмешательства в строительств пирамид, кроме того субъективного впечатления, которое они производят, просто нет. Это была бы крайне захватывающая и волнующая теория, но принять ее на веру мы не можем. Настоящий ученый должен стремиться к объективному познанию мира таким какой он есть, основываясь на фактах. Поэтому, как говорится, хотелось бы верить, но верится с трудом.
 Возможно так оно и было |  Ну или так |
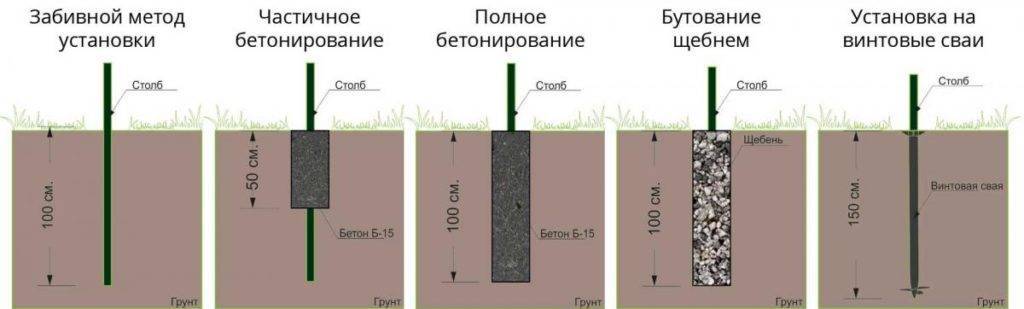
Разметка под фундамент своими руками
Качество постройки в огромной степени зависит от того, насколько правильно была выполнена разметка под фундамент
Занимаясь этой работой важно с максимальной точностью выдержать все прямые углы. Разметка фундамента своими руками под частный дом может быть выполнена несколькими способами. Чаще всего используются метод «египетского» треугольника и метод двух кривых
Поэтому в этой статье рассмотрим именно их
Чаще всего используются метод «египетского» треугольника и метод двух кривых. Поэтому в этой статье рассмотрим именно их.
Какие инструменты понадобятся?
Производится разметка фундамента своими руками с применением инструментов:
- Рулетки;
- Шнура;
- Гидроуровня и отвеса;
- Помимо этого понадобятся деревянные колышки.
С чего начать разметку?
Итак, как провести разметку фундамента? Для начала следует определить две исходные точки, вбив колышки по углам будущего здания, находящимся на одной прямой со стороны его самой длинной стены. Далее от них нужно будет провести перпендикуляры, таким образом отметив внешний контур смежных стен.
«Египетский треугольник». Самый простой метод
Разметка фундамента своими руками быстрее всего может быть произведена методом «золотого» треугольника, имеющего соотношение длин сторон 5*3*4. Мероприятие при этом выполняется в несколько этапов:
1. Для начала нужно найти длинную веревку и завязать на ней четыре узла. Первый – на конце, второй на расстоянии 3м, третий в четырех метрах от второго и последний в пяти метрах от третьего; 2. После этого самый первый и самый последний узлы соединяют гвоздем. По гвоздю следует вбить и в каждый из промежуточных узлов; 3. При этом длинную сторону получившегося треугольника нужно расположить вдоль линии между двумя уже вбитыми колышками; 4. Вдоль короткой стороны проводят требуемый перпендикуляр; 5. На полученной прямой, вбивают третий колышек на расстоянии равном ширине здания.
Важно: Правильность всех замеров следует обязательно проверить. Для этого между вбитыми кольями по диагоналям натягивают два шнура и связывают в месте пересечения
Paste a VALID AdSense code in Ads Elite Plugin options before activating it.
Метод двух дуг
Разметка фундамента своими силами этим методом выполняется также с использованием веревки. Предварительно от одного из колышков в обе стороны по уже имеющейся прямой отмеряют равные расстояния и отмечают найденные места. Далее к одной из полученных точек прикрепляют веревку с привязанным на противоположном конце гвоздем. Натянув ее проводят дугу напротив того колышка, от которого отмерялись расстояния. Затем веревку крепят ко второму отмеченному месту и чертят еще одну дугу. Из той точки, где дуги пересекутся, проводят линию к колышку. В результате получается прямой угол между ней и уже имеющейся линией.
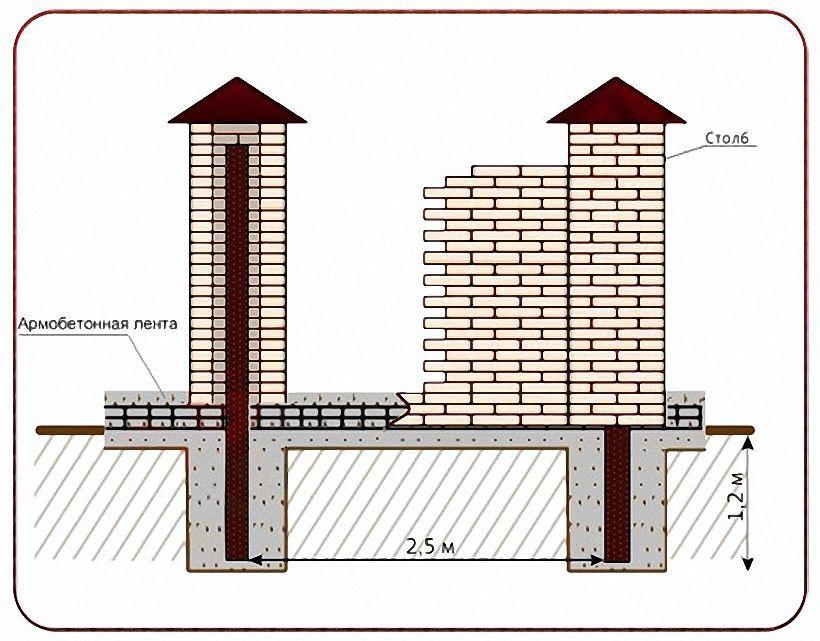
На заключительном этапе к кольям на высоте будущего фундамента привязывают шнур, поверяя горизонтальность его положения со всех четырех сторон, пользуясь строительным уровнем. Для ленточного фундамента чертят внутренний контур параллельно найденному внешнему и также натягивают шнур.
Совет: В том случае, если траншею предполагается копать с привлечением техники, шнуры лучше не использовать. В процессе работы они могут порваться. Линии между найденными точками в этом случае стоит прочертить песком. Для нахождения центров столбов столбчатого фундамента, от найденных углов вдоль прочерченных линий отмеряют необходимые расстояния и ставят отметки. Далее проверяют прямоугольность углов, получившихся на пересечении линий (соединяющей полученные точки на противоположных сторонах и линии периметра, на которой расположены отметки).
Разметка фундамента своими руками, как можно было заметить – процедура не такая уж и сложная. Самое главное, делать все аккуратно, хорошо натягивать веревку и обязательно проверять полученный результат методом диагоналей.
История
Название треугольнику с таким отношением сторон дали эллины: в VII—V веках до нашей эры древнегреческие философы и математики совершали путешествия в Египет. Так, например, Пифагор в 535 году до нашей эры по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно решение задачи по удвоению площади квадрата с помощью построения на его диагонали бóльшего квадрата привела Пифагора к доказательству знаменитой теоремы. Второй квадрат содержит четыре «половинки» первого, следовательно, его площадь вдвое больше. Эта задача легла в основу характерного для античного искусства способа пропорционирования. Такой способ гармонизации пропорций описал Древнегреческий философ Платон (ок. 427—347 гг. до н. э.).
Такой же приём, если верить Плинию Старшему (23—79 гг. н. э.) и Марку Теренцию Варрону (116—27 гг. до н. э.), использовал знаменитый древнегреческий скульптор Поликлет из Аргоса в сочинении «Канон» (сочинение не сохранилось).
Глупая ошибка строителей
«Египетский треугольник» действительно может помочь в разметке периметра фундамента, однако применение этого метода требует сохранения чётких пропорций. Небольшое отклонение от них − и угол уже не будет прямым. А это приведёт к разнице длин стен. Не единичны случаи, когда при идеальном совпадении длин диагоналей стены получаются разными. Ведь если вдуматься, то трапеция также подходит под заданные параметры, её диагонали равны, в то время как верхняя и нижняя сторона имеют разные длины.
ФОТО: youc.irПравильная трапеция также имеет одинаковые длины диагоналей, однако на квадрат она явно не тянет
Египетский треугольник в строительстве
Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.
Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника. Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
Стороны конструкции имеют следующее соотношение друг к другу:
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
- 5,
- 4,
Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.
Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов. Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять
В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять
Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять
Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.
Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.
Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам
Альтернативные способы построить прямой угол на 90 градусов
Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.
Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.
Как получить египетский треугольник при помощи верёвки
Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.
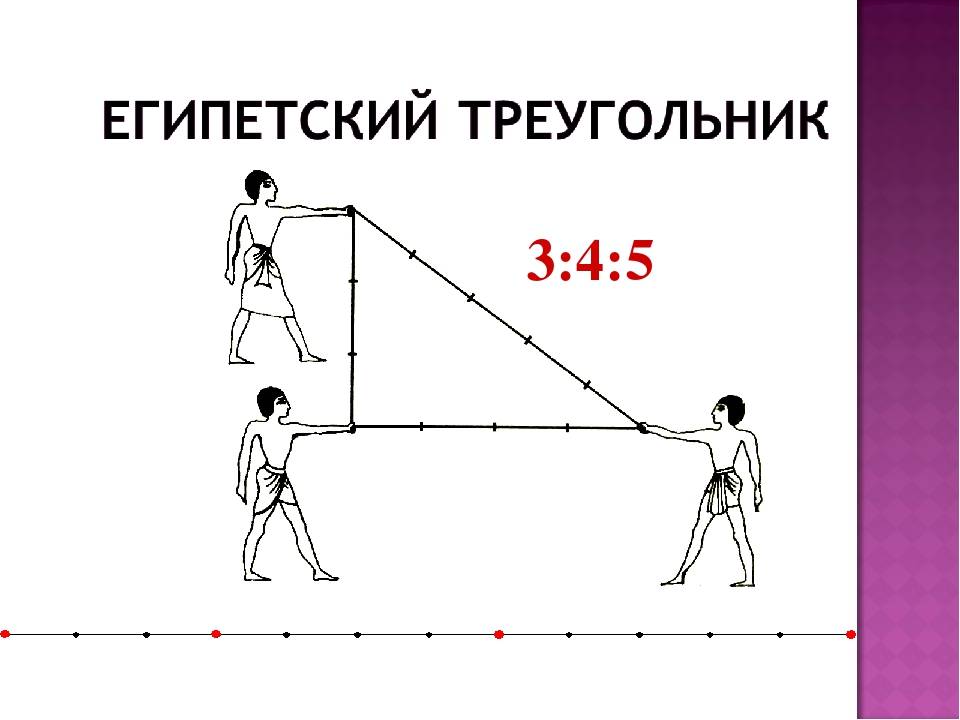
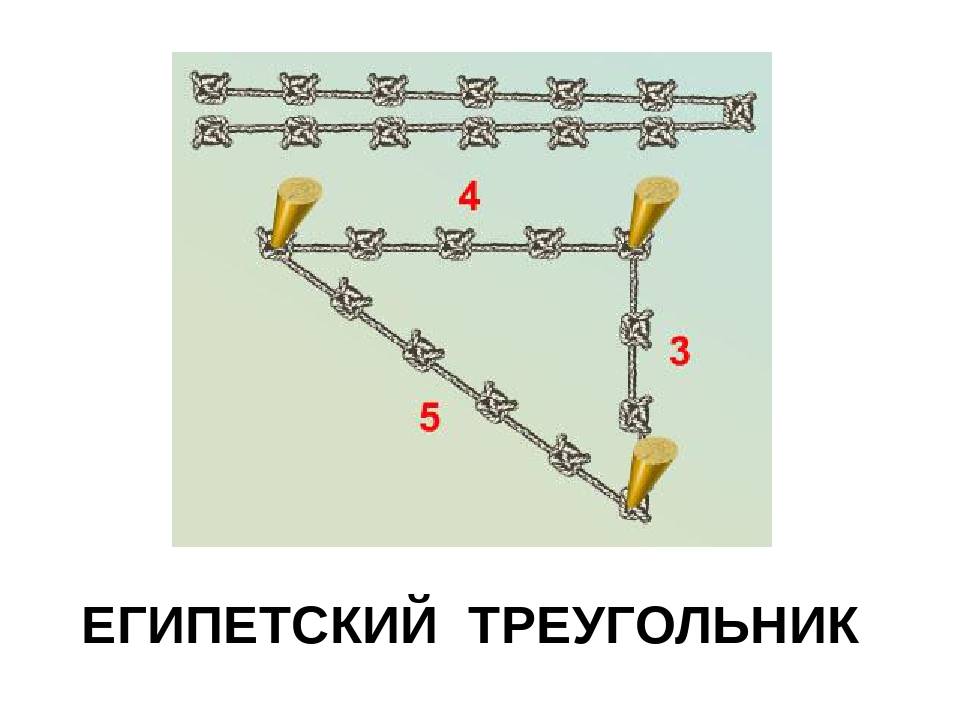
Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.
Как построить угол в 45, 30 и 60 градусов
Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.
Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол. Края должны совпасть
Края должны совпасть.
Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.
Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках
Особенности применения египетского треугольника в строительстве
Свойства такой геометрический конструкции, которая в полной мере уникальна, заключаются в том, что ее выстраивание без использования каких-то инструментов дает возможность выстраивать дома с правильными во всех планах углами
Крайне важно, что в идеале стоит применять угольник или транспортир
Итак, свойства египетского треугольника дает возможность делать правильные в каждом соотношении углы. Стороны конструкции обладают таким соотношением друг к другу, как 5:4:3. Чтобы проверять те или иные фигуры были начерчены, требуется применять хорошо известную теорему Пифагора, которую каждый человек знает со школьных времен.
Интересно, что правило египетского треугольника таково, что квадрат гипотенузы равен квадратам катетов (двух).
Альтернативные методы выстраивания прямого угла
Как уже было упомянуто выше, самым лучшим вариантом будет лишь взять угольник или транспортир. Такие инструменты дают возможность с минимальными затратами сил и времени добиваться требуемых пропорций. Главным же свойством треугольника является его универсальность. Фигуру можно выстраивать, не имея в арсенале почти ничего.
Как сделать египетский треугольник с применением веревки
Египетский треугольник в строительстве крайне важен, и его качества тяжело переоценить. Неудивительно, что древними инженерами было придумано большое количество методов ее образования с применением минимальных ресурсов. Одним из наиболее простых может считаться способ образования египетского треугольника со всеми свойствами, которые вытекают при помощи обычной веревки. Требуется взять бечевку и разрезать ее на 12 идеально равных частей. Из них требуется сложить фигуру, которая обладает пропорциями 3:4:5.
Как выстраивать углы на 30, 45 и 60 градусов
Естественно, что треугольники египетского типа и его качества весьма полезные при строительстве дома. но без остальных углов вам не удастся обойтись. Чтобы получился угол, который равен 45 градусам, требуется взять материал багета или рамки
После этого важно распиливать его под углом в 45 градусов и состыковать половинки друг с другом
Обратите внимание, что для получения требуемого наклона требуется вырвать лист бумаги из журнала, а после согнуть его. При этом линия изгиба будет проходить через угол, и края обязательно должна совпадать
Как добраться?
Быстрее всего добраться к Египетскому мосту в Санкт-Петербурге можно от станции метро «Балтийская». Нужно выйти на этой станции и проследовать на Обводный канал. Оттуда свернуть на Лермонтовский проспект, по которому нужно пройти еще минут 10-15. Вдали появятся очертания известных зеленых обелисков под светом фонарей, и там же – фигуры сфинксов, охраняющих вход на мост.
Если есть немного свободного времени и желания пройтись, также можно выйти на станции «Технологический Институт», оттуда перейти на 1-ю Красноармейскую, а затем свернуть на проспект Троицкий. Так можно будет по дороге посмотреть Троицкий собор Санкт-Петербурга.
Адрес: г. Санкт-Петербург, Набережная реки Фонтанки, 151-153.
 Watch this video on YouTube
Watch this video on YouTube
Применение египетского треугольника
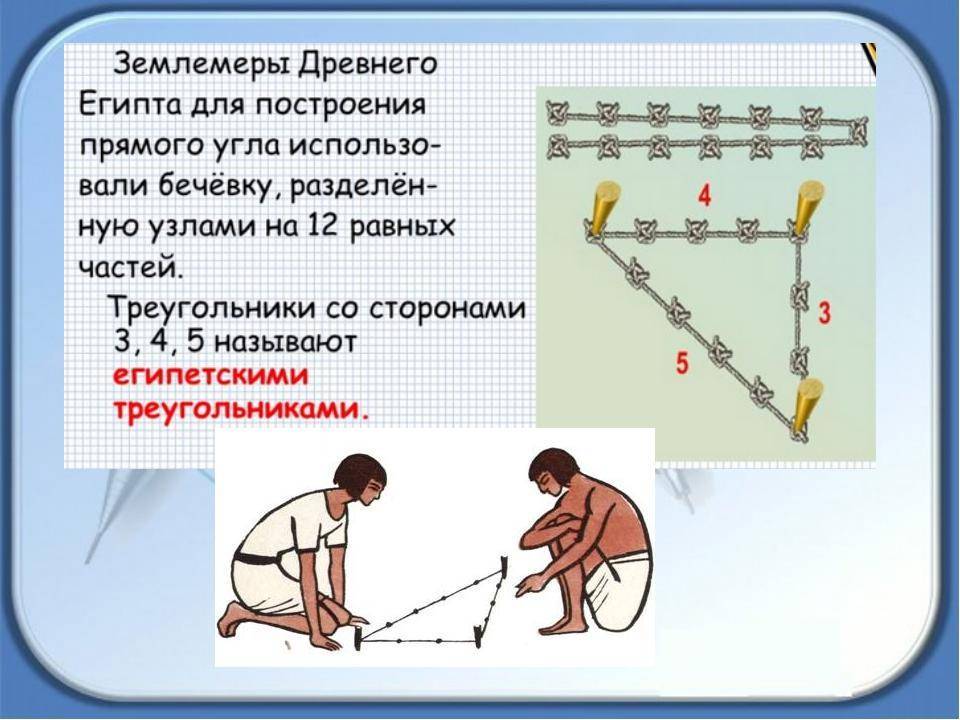
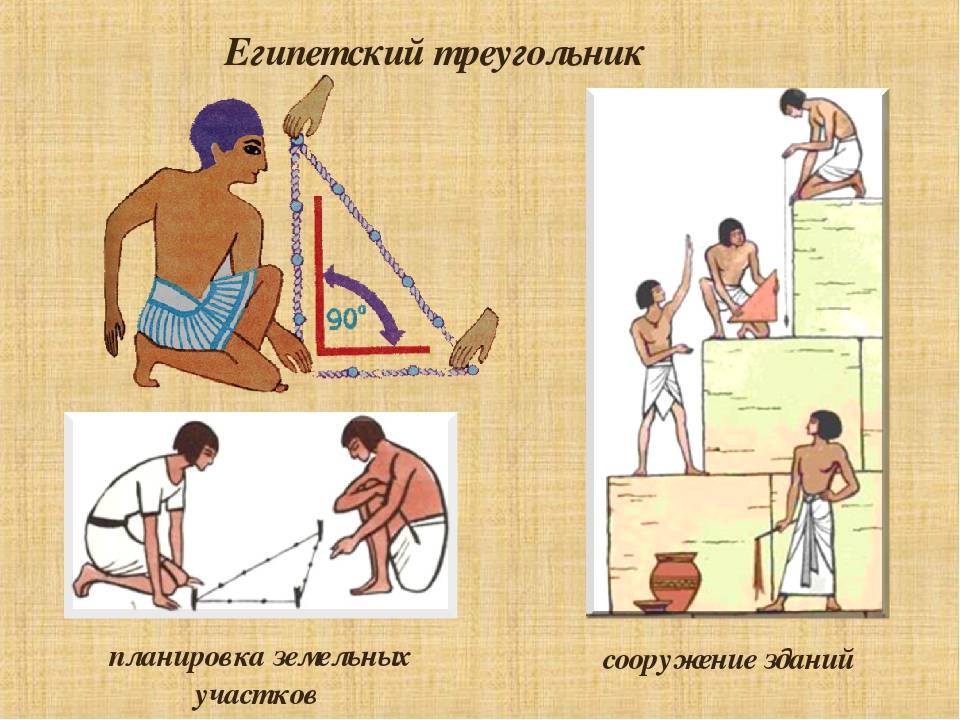
В Древние века в архитектуре и строительстве египетский треугольник пользовался огромной популярностью. Особенно он был необходим, если для построения прямого угла использовали веревку или шнур.
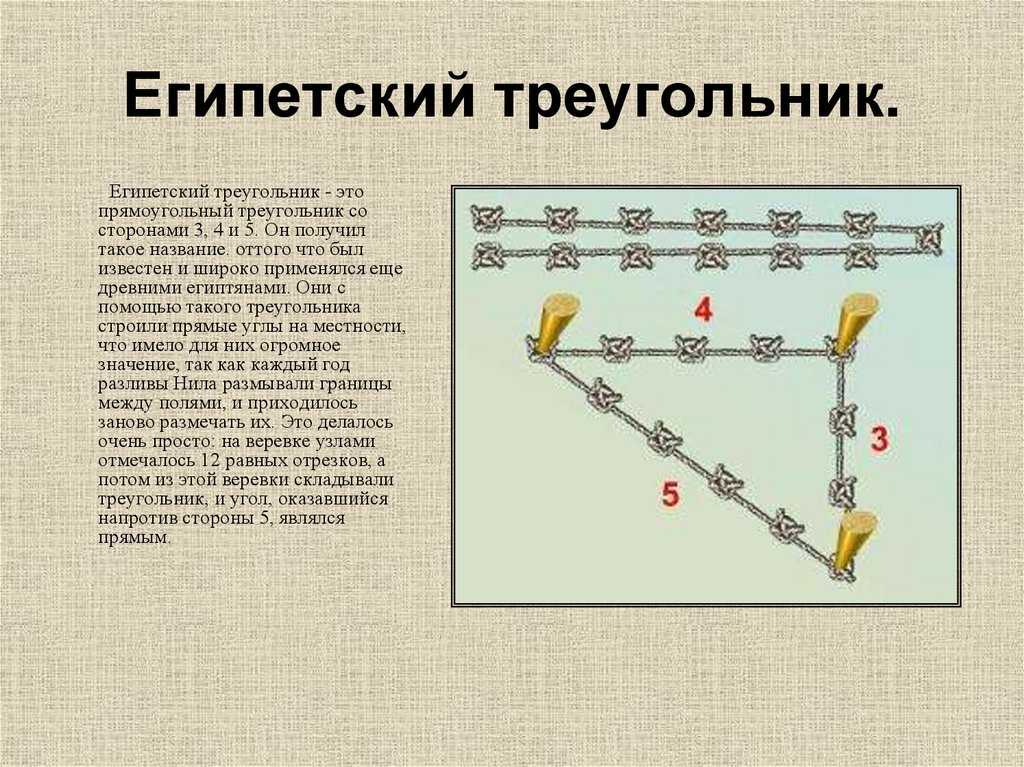
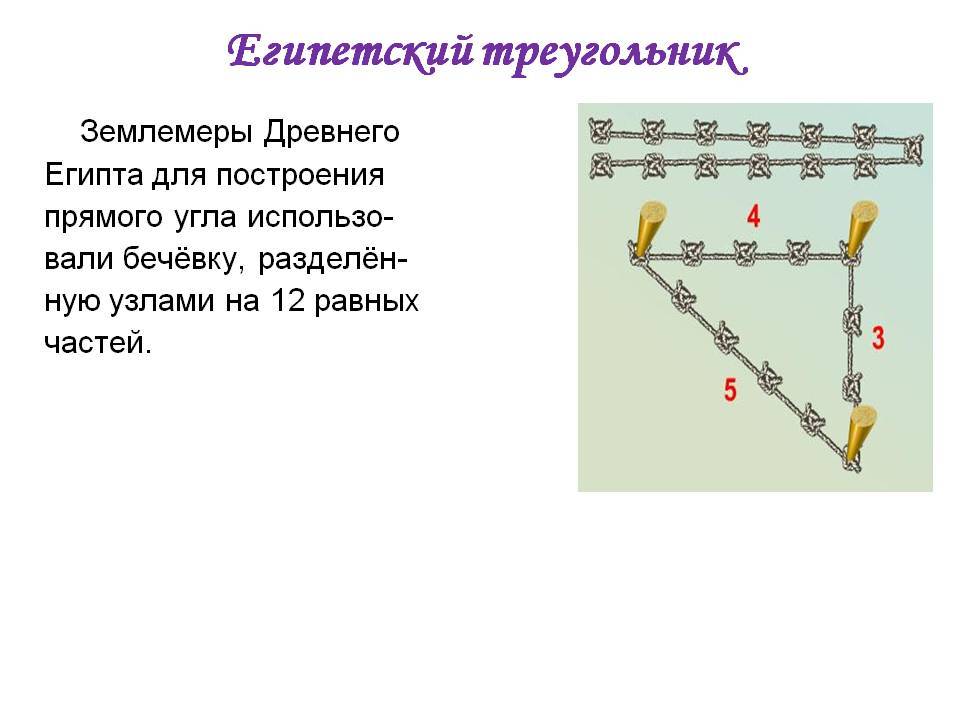
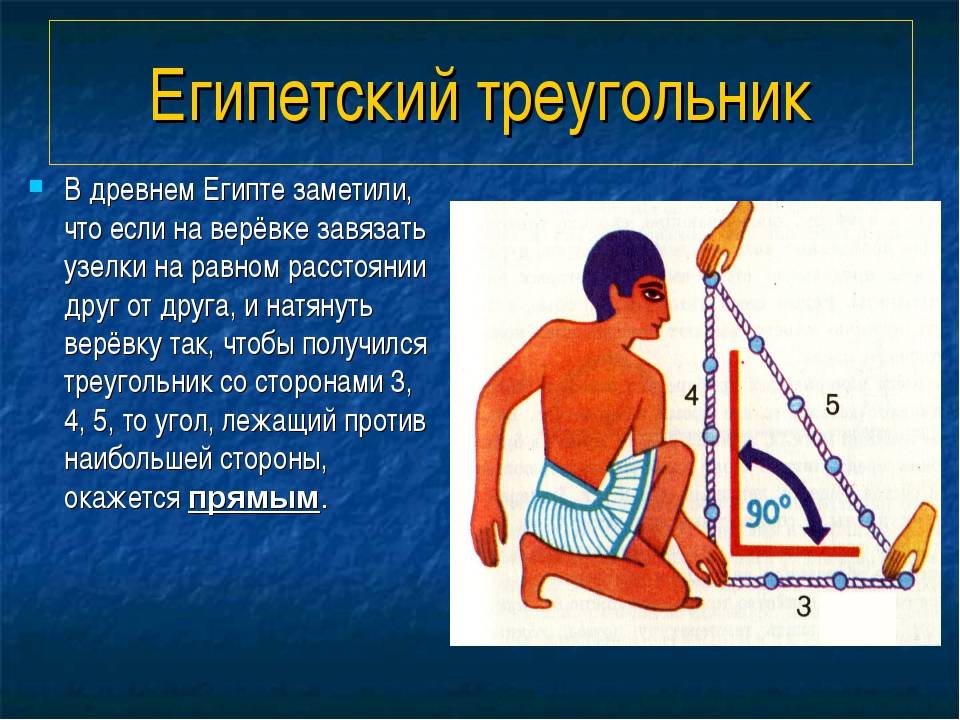
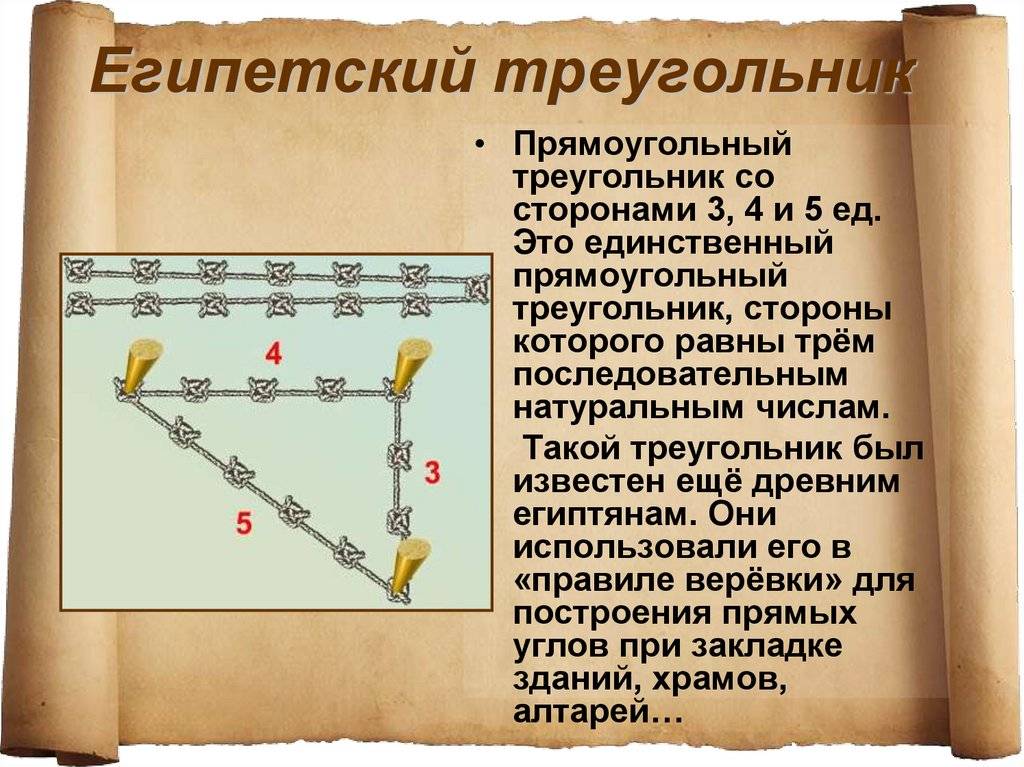
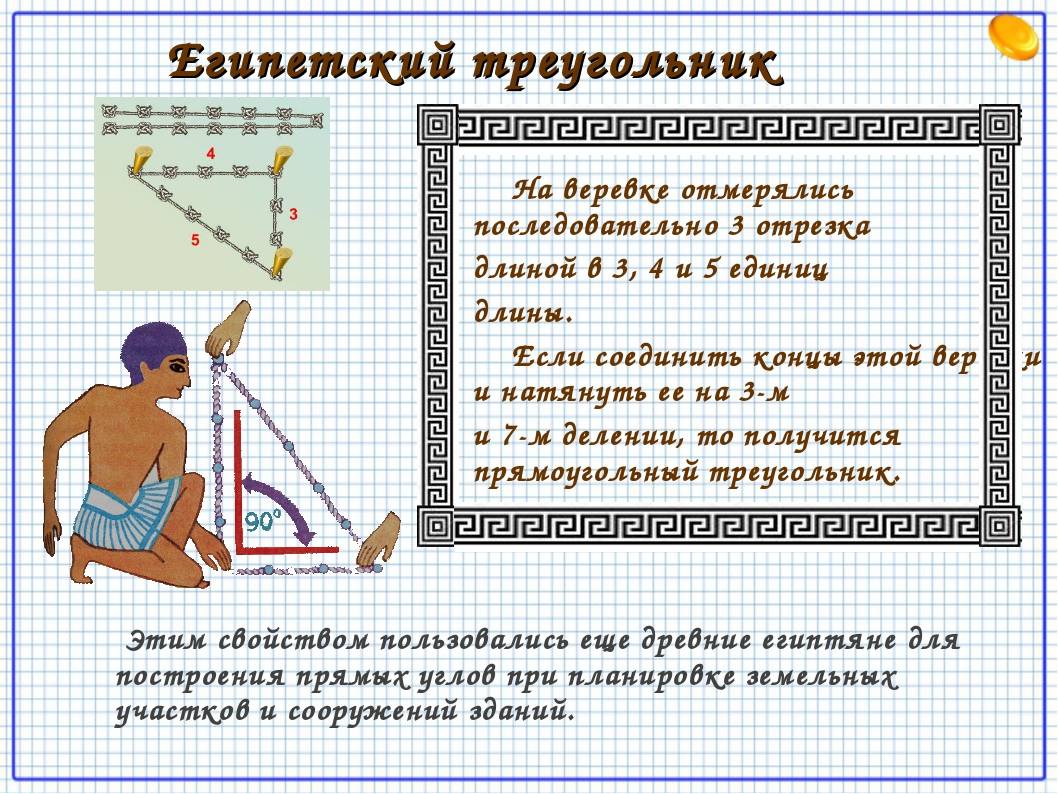
Ведь известно, что отложить прямой угол в пространстве, является довольно таки сложным занятием и поэтому предприимчивые египтяне изобрели интересный способ построения прямого угла. Для этих целей они брали веревку, на которой отмечали узелками двенадцать ровных частей и потом с этой веревки складывали треугольник, со сторонами, которые равнялись 3 , 4 и 5 частям и в итоге без проблем, получали прямоугольный треугольник. Благодаря такому замысловатому инструменту, египтяне с огромной точностью размеряли землю для сельскохозяйственных работ, строили дома и пирамиды.
Вот так посещение Египта и изучение особенностей египетской пирамиды подтолкнуло Пифагора на открытие своей теоремы, которая, кстати, попала в Книгу Рекордов Гиннеса, как теорема, которая имеет самое большое количество доказательств.
Треугольные колеса Рело
Колесо— круглый (как правило), свободно вращающийся или закреплённый на оси диск, позволяющий поставленному на него телу катиться, а не скользить. Колесо повсеместно используется в различных механизмах и инструментах. Широко применяется для транспортировки грузов.
Колесо существенно уменьшает затраты энергии на перемещение груза по относительно ровной поверхности. При использовании колеса работа совершается против силы трения качения, которая в искусственных условиях дорог существенно меньше, чем сила трения скольжения. Колёса бывают сплошные (например, колёсная пара железнодорожного вагона) и состоящие из довольно большого количества деталей, к примеру, в состав автомобильного колеса входит диск, обод, покрышка, иногда камера, болты крепления и тд. Износ покрышек автомобилей является почти решённой проблемой (при правильно установленных углах колёс). Современные покрышки проезжают свыше 100 000 км. Нерешённой проблемой является износ покрышек у колёс самолётов. При соприкосновении неподвижного колеса с бетонным покрытием взлётной полосы на скорости в несколько сотен километров в час износ покрышек огромен.
- В июле 2001 года на колесо был получен инновационный патент со следующей формулировкой: «круглое устройство, применяемое для транспортировки грузов». Этот патент был выдан Джону Кэо, юристу из Мельбурна, который хотел тем самым показать несовершенство австралийского патентного закона .
- Французская компания Мишлен в 2009 году разработала пригодное к массовому выпуску автомобильное колесо Active Wheel со встроенными электродвигателями, приводящими в действие колесо, рессору, амортизатор и тормоз. Таким образом, эти колёса делают ненужными следующие системы автомобиля: двигатель, сцепление, коробку передач, дифференциал, приводной и карданный валы.
- В 1959 году американец А. Сфредд получил патент на квадратное колесо. Оно легко шло по снегу, песку, грязи, преодолевало ямы. Вопреки опасениям, машина на таких колёсах не «хромала» и развивала скорость до 60 км/ч.
Франц Рело (Franz Reuleaux, 30 сентября 1829 — 20 августа 1905) — немецкий инженер-механик, лектор Берлинской Королевской Технической академии, ставший впоследствии ее президентом. Первым, в 1875 году, разработал и изложил основные положения структуры и кинематики механизмов; занимался проблемами эстетичности технических объектов, промышленным дизайном, в своих конструкциях придавал большое значение внешним формам машин. Рело часто называют отцом кинематики.
Египетский треугольник, его свойства
О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.
История египетского треугольника
Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.
Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.

Египетский треугольник в строительстве
Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
- 5,
- 4,
- 3.
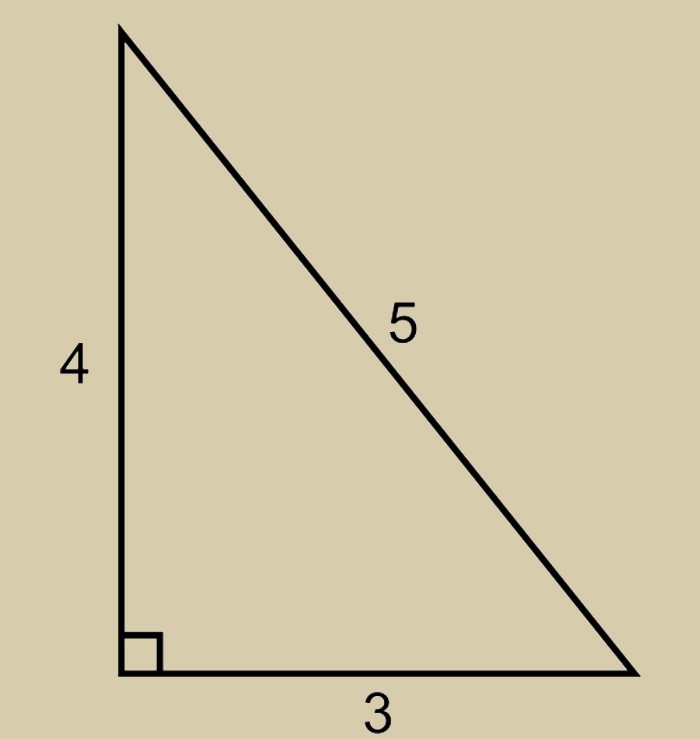
Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.
Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.
Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.
Альтернативные способы построить прямой угол на 90 градусов
Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.
Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.
Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.
Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.
Как построить угол в 45, 30 и 60 градусов
Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.
Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.
Итоги

Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.
Комментарии
История создания Египетского моста
Первоначально по своей конструкции это был цепной мост, появившийся один из первых в своем роде в Санкт-Петербурге. В то время, а именно в конце XVIII – в начале XIX веков, только зарождалась идея создания таких конструкций, причем одновременно сразу в нескольких развитых странах.
Тогда только начинали использовать металл в строительстве, учитывая большую гибкость металлических сплавов по сравнению с чугуном. Таким образом, конструкторы XVIII века задумали новый формат переправы через реку – подвесное полотно на железных цепях.
Пионером в Санкт-Петербурге, а также одной из первых конструкций подобного типа был мост под названием Екатерингофский, который, к сожалению, уже не существует. В 1823 году начали строить второй, аналогичный мост – Патнелемоновский, и сразу же приступили к созданию Египетского моста, соединяющего два берега Фонтанки.
В начале XIX века во всем мире пользовалась большой популярностью тема изучения востока, и, в первую очередь, Древнего Египта. В архитектуре Петербурга это увлечение отразилось в виде фонтанов возле Пулковской горы, украшенных сфинксами. В Царском селе имеются ворота в Египетском стиле, а прямо напротив Академии художеств стоят известные всем сфинксы.
К сожалению, точной даты начала конструирования Египетского моста в Спб не сохранилось. Известно только, что в начале 1825 года уже был указ от главнокомандующего путей сообщений Питера, герцога герцог А. Вюртембергского, о необходимости срочного завершения процесса проектирования.
Вниманию герцога были предложены два варианта конструкций с разными сметами, однако оба не подошли из-за показавшейся начальству дороговизны проекта. В итоге к исполнению взяли третий вариант, самый упрощенный, по которому переправа строилась по минимальному расстоянию между берегами Фонтанки, не учитывая географию прилегающих улиц.
Работы велись не так быстро, как хотелось бы. Задержку в основном вызывали постоянные отсрочки каменных работ. В итоге для гранитных устоев моста был использован тот же гранит, что и для облицовки Михайловского замка. Проект предусматривал окончание работ до декабря 1825 года, но итоговые сроки сдачи были перенесены почти на год.
Так как мост не был самым первым в Питере, и у конструкторов уже имелся некоторый опыт, его конструкция представляла собой более легкую конструкцию Пантелеймоновского моста его улучшенный вариант. Поддерживали его три цепи, а порталы были украшены египетскими иероглифами. Также в украшении использовалась позолота.
Трудами П.П. Соколова были созданы чугунные фигуры сфинксов, установленные на пьедесталах возле мостовых устоев. Первоначально создали пару тестовых фигур, которые оставались долгое время в запасе. Уже во второй половине XX века они нашли свое применение на пристани возле Каменноостровского моста.
Угловой
Специальные угловые треугольники, вписанные в единичный круг, удобны для визуализации и запоминания тригонометрических функций, кратных 30 и 45 градусам.
Специальные прямоугольные треугольники «на основе углов» определяются соотношением углов, из которых состоит треугольник. Углы этих треугольников таковы, что больший (прямой) угол, который составляет 90 градусов илиπ2 радиан равен сумме двух других углов.
Длины сторон обычно вычисляются на основе единичной окружности или других геометрических методов. Такой подход можно использовать для быстрого воспроизведения значений тригонометрических функций для углов 30 °, 45 ° и 60 °.
Специальные треугольники используются для помощи в вычислении общих тригонометрических функций, как показано ниже:
| градусы | радианы | углы | повороты | грех | потому что | загар | котан |
|---|---|---|---|---|---|---|---|
| 0 ° | 0 г | √ 2 = 0 | √ 42 = 1 | неопределенный | |||
| 30 ° | π6 | 33 +13грамм | 112 | √ 12 знак равно 12 | √ 32 | 1√ 3 | √ 3 |
| 45 ° | π4 | 50 г | 18 | √ 22 знак равно 1√ 2 | √ 22 знак равно 1√ 2 | 1 | 1 |
| 60 ° | π3 | 66 +23грамм | 16 | √ 32 | √ 12 знак равно 12 | √ 3 | 1√ 3 |
| 90 ° | π2 | 100 г | 14 | √ 42 = 1 | √ 2 = 0 | неопределенный |
45 ° –45 ° –90 °
30 ° –60 ° –90 °
Треугольник 45 ° –45 ° –90 °, треугольник 30 ° –60 ° –90 ° и равносторонний / равносторонний (60 ° –60 ° –60 °) треугольник — это три треугольника Мёбиуса на плоскости, что означает, что они разбейте плоскость мозаикой с помощью отражений в их сторонах; см. группу «Треугольник» .
45 ° –45 ° –90 ° треугольник
Установить квадрат
Длины сторон треугольника 45 ° –45 ° –90 °
В плоской геометрии построение диагонали квадрата приводит к треугольнику, три угла которого находятся в соотношении 1: 1: 2, что в сумме дает 180 ° или π радиан. Следовательно, углы составляют соответственно 45 ° (π4), 45 ° (π4) и 90 ° (π2). Стороны этого треугольника находятся в соотношении 1: 1: √ 2 , что непосредственно следует из теоремы Пифагора .
Из всех прямоугольных треугольников треугольник 45 ° –45 ° –90 ° имеет наименьшее отношение гипотенузы к сумме катетов, а именно √ 22. и наибольшее отношение высоты от гипотенузы к сумме катетов, а именно√ 24.
Треугольники с этими углами — единственные возможные прямоугольные треугольники, которые также являются равнобедренными треугольниками в евклидовой геометрии . Однако в сферической геометрии и гиперболической геометрии существует бесконечно много различных форм прямоугольных равнобедренных треугольников.
Треугольник 30 ° –60 ° –90 °
Установить квадрат
Стороны треугольника 30 ° –60 ° –90 °
Это треугольник, три угла которого находятся в соотношении 1: 2: 3 и составляют соответственно 30 ° (π6), 60 ° (π3) и 90 ° (π2). Стороны находятся в соотношении 1: √ 3 : 2.
Доказательство этого факта ясно с помощью тригонометрии . Геометрическое доказательство:
- Нарисуйте равносторонний треугольник ABC со стороной 2 и точкой D в качестве середины отрезка BC . Нарисуйте линию высоты от A до D . Тогда ABD — это треугольник 30 ° –60 ° –90 ° с гипотенузой длины 2 и основанием BD длины 1.
- Тот факт, что оставшаяся катета AD имеет длину √ 3, немедленно следует из теоремы Пифагора .
Треугольник 30 ° –60 ° –90 ° — единственный прямоугольный треугольник, углы которого находятся в арифметической прогрессии. Доказательство этого факта простое и следует из того факта, что если α , α + δ , α + 2 δ — углы в прогрессии, то сумма углов 3 α + 3 δ = 180 °. После деления на 3 угол α + δ должен составлять 60 °. Прямой угол равен 90 °, а оставшийся угол равен 30 °.