Онлайн калькулятор расчета делителя напряжения

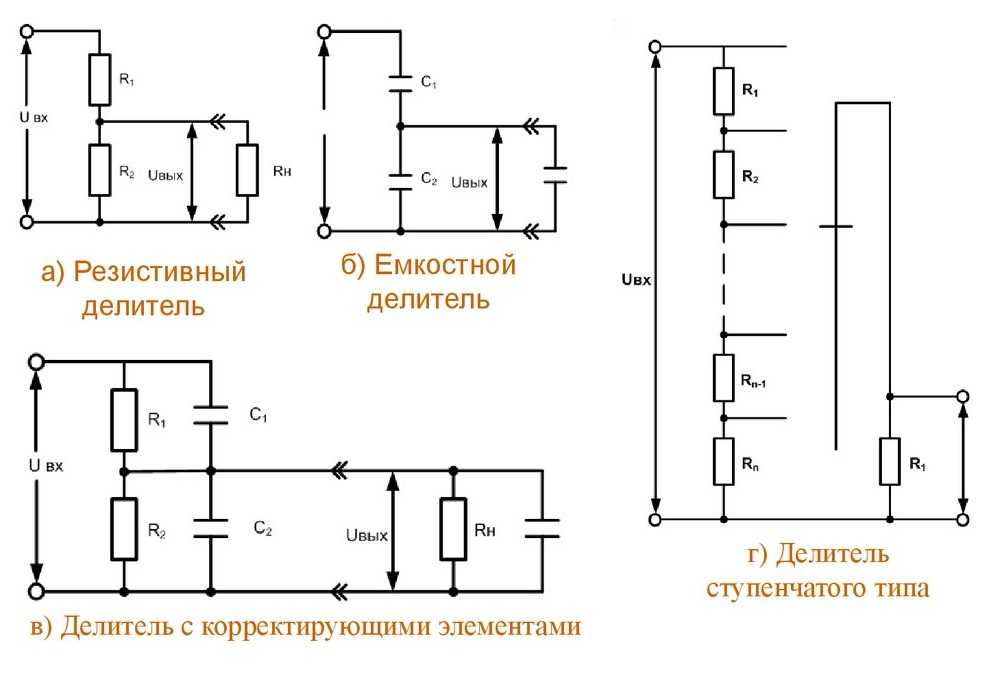
Использование операционных усилителей

Как известно, у диодов вольтамперная характеристика нелинейная, создавая однофазный прецизионный (высокоточный) выпрямитель двухполупериодного типа на микросхеме ОУ, можно существенно снизить погрешность. Помимо этого, имеется возможность создать преобразователь, позволяющий стабилизировать ток на нагрузке. Пример схемы такого устройства показан ниже.

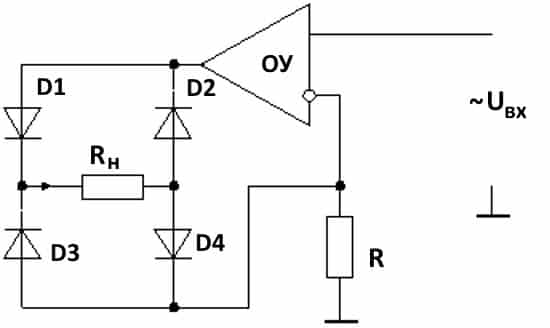
На рисунке изображен простейший стабилизатор тока. Используемый в нем ОУ – это управляемый по напряжению источник. Такая реализация позволяет добиться, чтобы ток на выходе преобразователя не зависел от потери напряжения на нагрузке Rн и диодном мосту D1-D4.

Если требуется стабилизация напряжения, схему преобразователя можно незначительно усложнить, добавив в нее стабилитрон. Он подключается параллельно сглаживающей емкости.

Применение

Использование такой схемотехники на практике демонстрируют следующие примеры. Для расчетов электрических параметров без учета сопротивления нагрузки подойдут рассмотренные выше ручные и автоматизированные методики.

Потенциометры

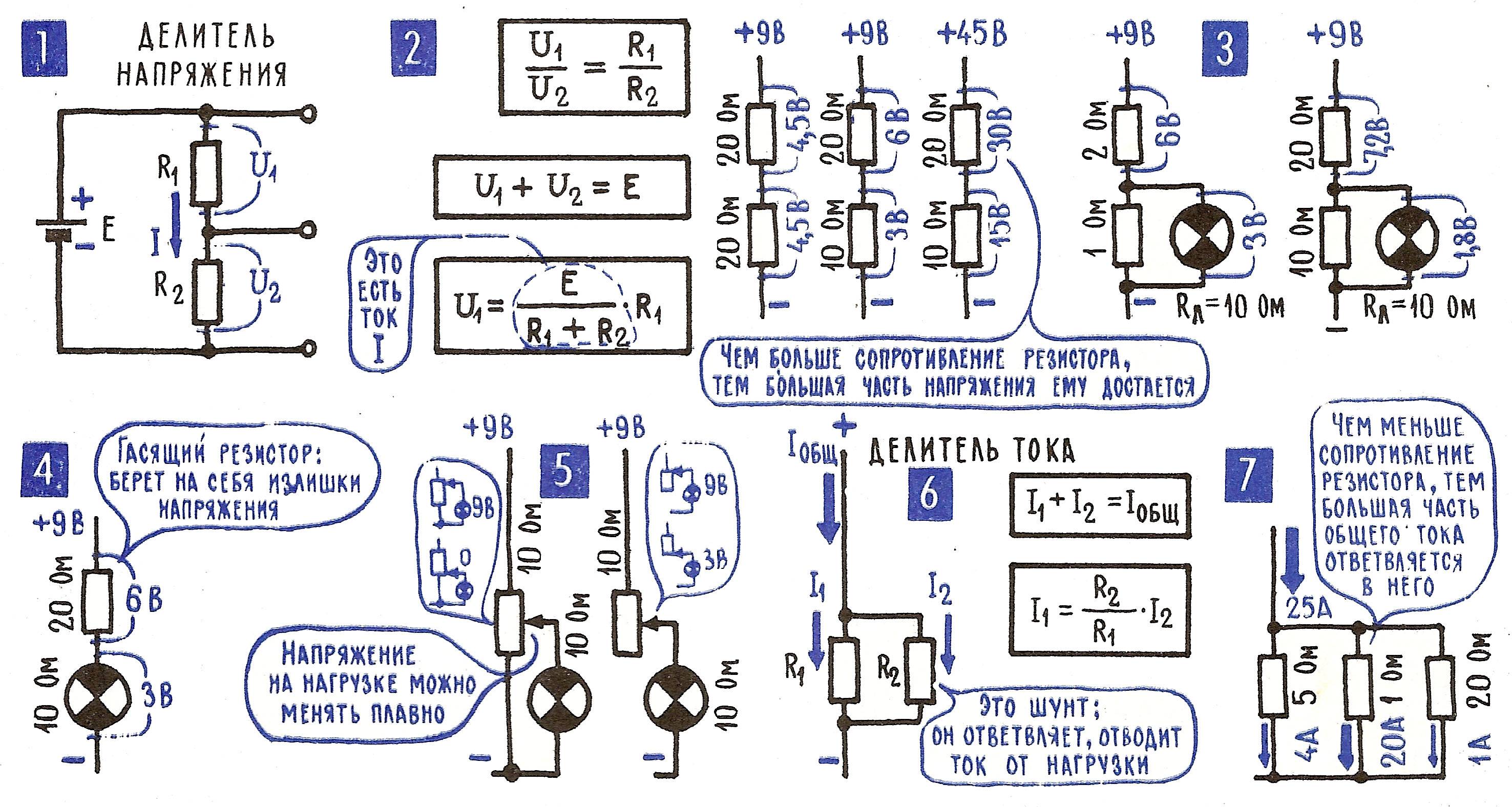
Если резистор оснастить ползунком и соответствующим приводом, сопротивления можно будет менять плавно. Это решение позволяет точнее менять напряжения на выходе, по сравнению с дискретными схемами. Главный недостаток – усложнение конструкции, что, кроме удорожания, снижает надежность. Приходится обеспечивать герметичность рабочей зоны для исключения загрязнения и предотвращения коррозийных процессов.

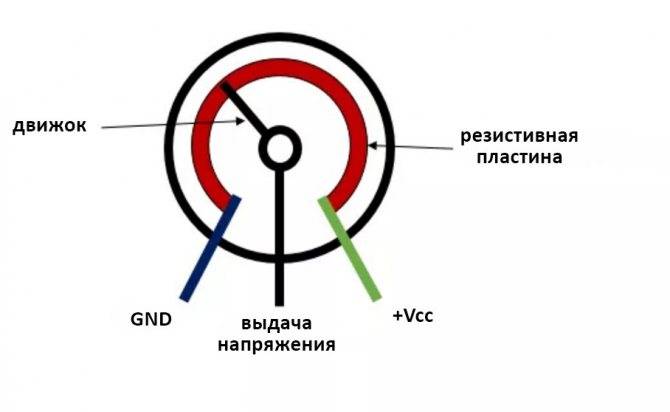
Принципиальная схема потенциометра

Резистивные датчики

В этом варианте пользуются способностью некоторых материалов увеличивать/ уменьшать электрическое сопротивление под воздействием температуры, светового потока, других внешних воздействий. Созданный на основе этих принципов датчик устанавливают в плечо делителя. По уровню напряжения на выходе контролируют изменение соответствующих параметров.

Цепи обратной связи в усилителях

Таким решением обеспечивают необходимый коэффициент усиления. На представленной ниже схеме этот параметр не будет никогда ниже единицы. Для повышения уровня преобразования увеличивают значение сопротивления R2 по отношению к R1.

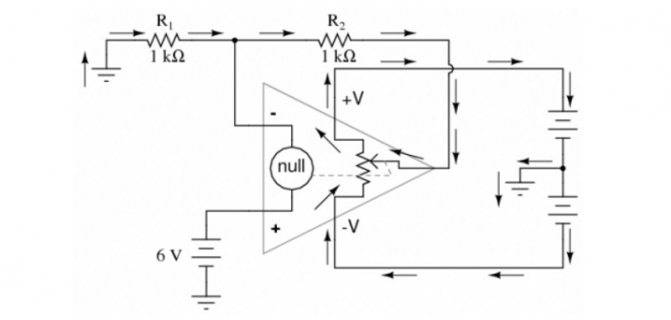
Делитель напряжения в цепи обратной связи

Простейшие электрические фильтры

Для фильтрации заменяют конденсатором резисторы R1 или R2. В первом варианте устройство беспрепятственно пропускает высокочастотные составляющие. При снижении частоты до определенного уровня реактивное сопротивление увеличивается, препятствует прохождению тока. Аналогичным образом делают изменения в нижнем плече делителя с целью отсечения низких частот.

Усилитель напряжения

Переменным резистором изменяют уровень сигнала для получения необходимой громкости звучания. В таких устройствах применяют элементы с логарифмической характеристикой изменения сопротивления, что хорошо соответствует естественному механизму восприятия человеческими органами слуха.

Параметрический стабилизатор напряжения

В таких схемах нижнее плечо делителя можно создать с применением стабилитрона. Его вольтамперные характеристики выбирают таким образом, чтобы выходное напряжение сохраняло нужное значение при изменении входных параметров.

Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях — Help for engineer

Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях

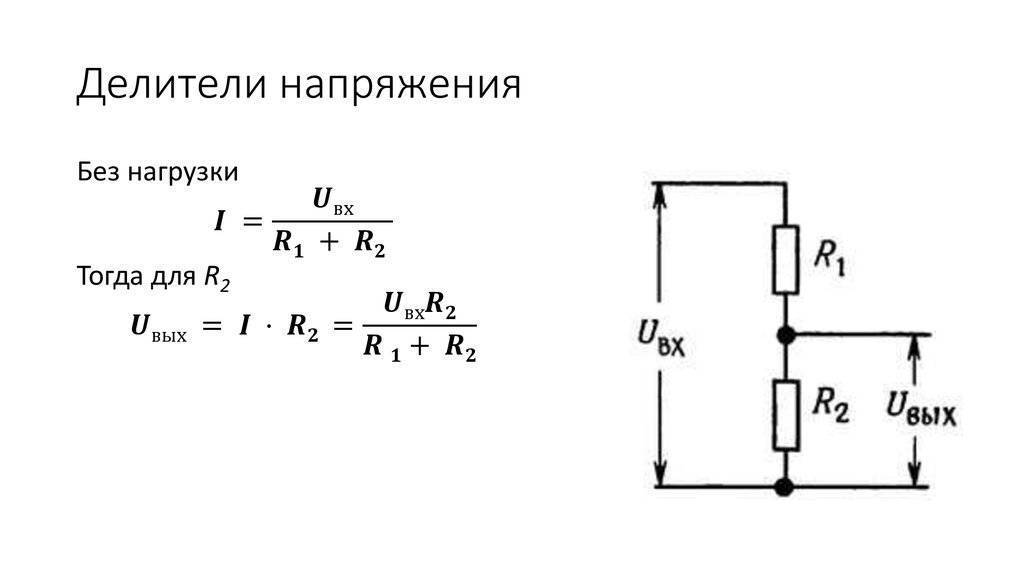
Делитель напряжения используется в электрических цепях, если необходимо понизить напряжение и получить несколько его фиксированных значений. Состоит он из двух и более элементов (резисторов, реактивных сопротивлений). Элементарный делитель можно представить как два участка цепи, называемые плечами. Участок между положительным напряжением и нулевой точкой – верхнее плечо, между нулевой и минусом – нижнее плечо.

Делитель напряжения на резисторах может применятmся как для постоянного, так и для переменного напряжений. Применяется для низкого напряжения и не предназначен для питания мощных машин. Простейший делитель состоит из двух последовательно соединенных резисторов:

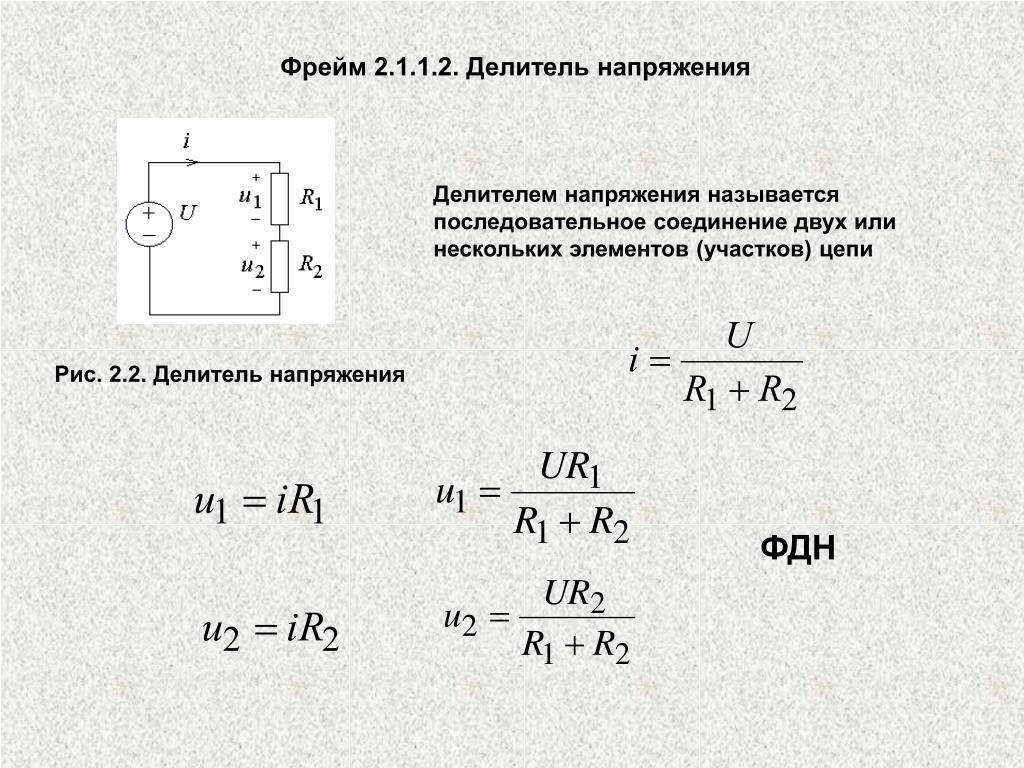
На резистивный делитель напряжения подается напряжение питающей сети U, на каждом из сопротивлений R1 и R2 происходит падение напряжения. Сумма U1 и U2 и будет равна значению U.

В соответствии с законом Ома (1):

Падение напряжения будет прямо пропорционально значению сопротивления и величине тока. Согласно первому закону Кирхгофа, величина тока, протекающего через сопротивления одинакова. С чего следует, что падение напряжения на каждом резисторе (2,3):

Тогда напряжение на всем участке цепи (4):

Отсюда определим, чему равно значение тока без включения нагрузки (5):

Если подставить данное выражение в (2 и 3), то получим формулы расчета падения напряжения для делителя напряжения на резисторах (6, 7):

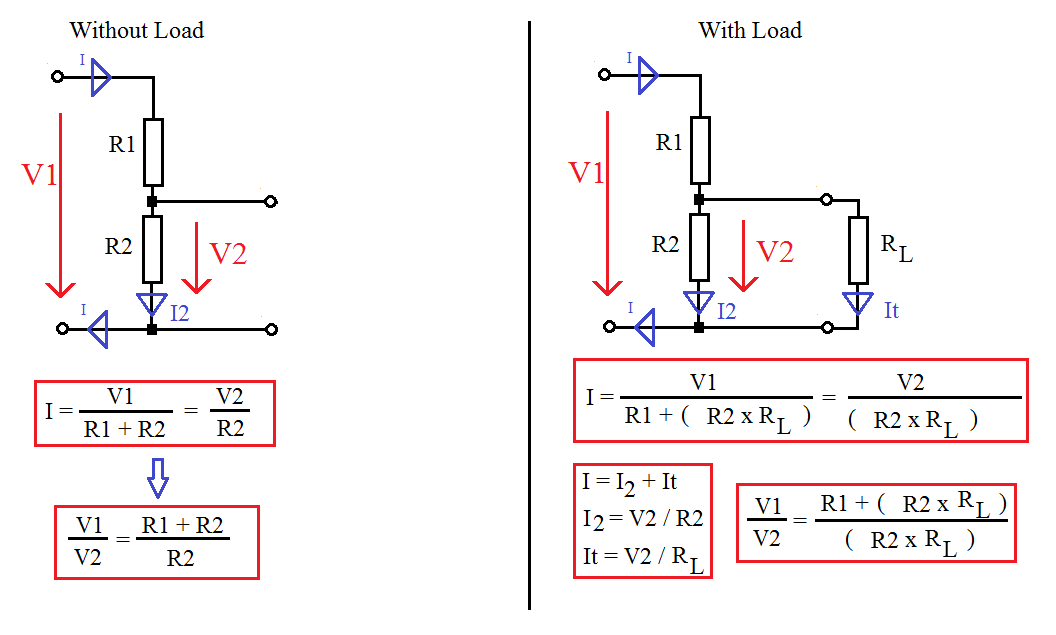
Необходимо упомянуть, что значения сопротивлений делителя должны быть на порядок или два (все зависит от требуемой точности питания) меньше, чем сопротивление нагрузки. Если же это условие не выполняется, то при приведенном расчете подаваемое напряжение будет посчитано очень грубо.

Для повышения точности необходимо сопротивление нагрузки принять как параллельно подсоединенный резистор к делителю. А также использовать прецизионные (высокоточные) сопротивления.

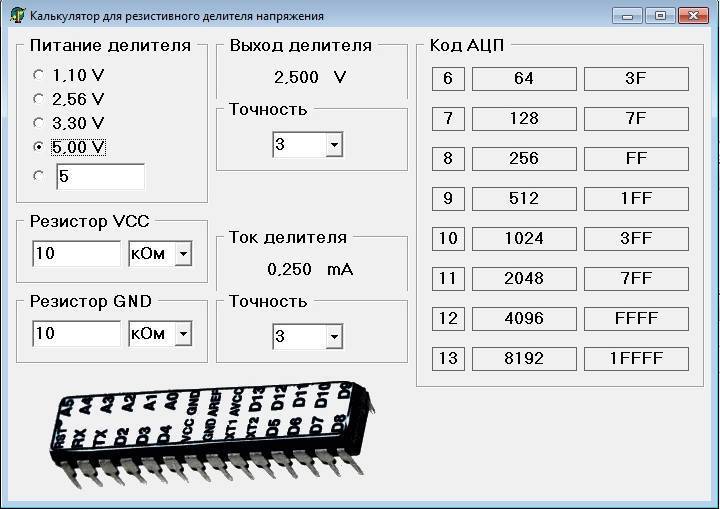
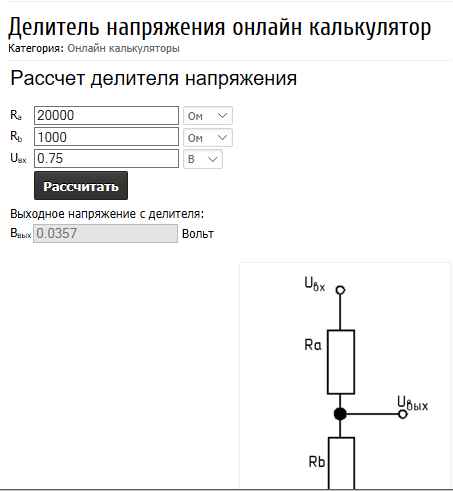
Онлайн подбор сопротивлений для делителя

Пусть источник питания выдает 24 В постоянного напряжения, примем, что величина сопротивления нагрузки переменная, но минимальное значение равно 15 кОм. Необходимо рассчитать параметры резисторов для делителя, выходное напряжение которого равно 6 В.

Таким образом, напряжения: U=24 B, U₂=6 В; сопротивление резисторов не должно превышать 1,5 кОм (в десять раз меньше значения нагрузки). Принимаем R1=1000 Ом, тогда используя формулу (7) получим:

выразим отсюда R₂:

Зная величины сопротивления обоих резисторов, найдем падение напряжения на первом плече (6):

Ток, который протекает через делитель, находится по формуле (5):

Схема делителя напряжения на резисторах рассчитана выше и промоделирована:

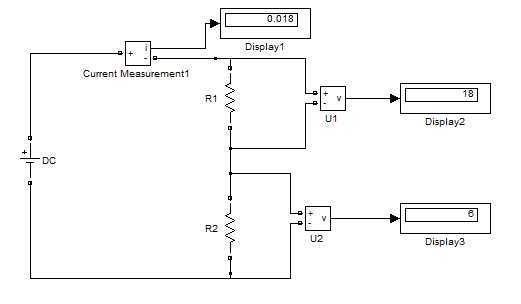
Использование делителя напряжения очень неэкономичный, затратный способ понижения величины напряжения, так как неиспользуемая энергия рассеивается на сопротивлении (превращается в тепловую энергию). КПД очень низкий, а потери мощности на резисторах вычисляются формулами (8,9):

По заданным условиям, для реализации схемы делителя напряжения необходимы два резистора:

		1. R1=1 кОм, P1=0,324 Вт.
		2. R2=333,3 Ом, P2=0,108 Вт.

Полная мощность, которая потеряется:

Делитель напряжения на конденсаторах применяется в схемах высокого переменного напряжения, в данном случае имеет место реактивное сопротивление.

Сопротивление конденсатора рассчитывается по формуле (10):

		где С – ёмкость конденсатора, Ф;
		f – частота сети, Гц.

Исходя из формулы (10), видно, что сопротивление конденсатора зависит от двух параметров: С и f. Чем больше ёмкость конденсатора, тем сопротивление его ниже (обратная пропорциональность). Для ёмкостного делителя расчет имеет такой вид (11, 12):

Еще один делитель напряжения на реактивных элементах – индуктивный, который нашел применение в измерительной технике. Сопротивление индуктивного элемента при переменном напряжении прямо пропорционально величине индуктивности (13):

где L – индуктивность, Гн.

Падение напряжения на индуктивностях (14,15):

Применимость

Делитель напряжения подходит

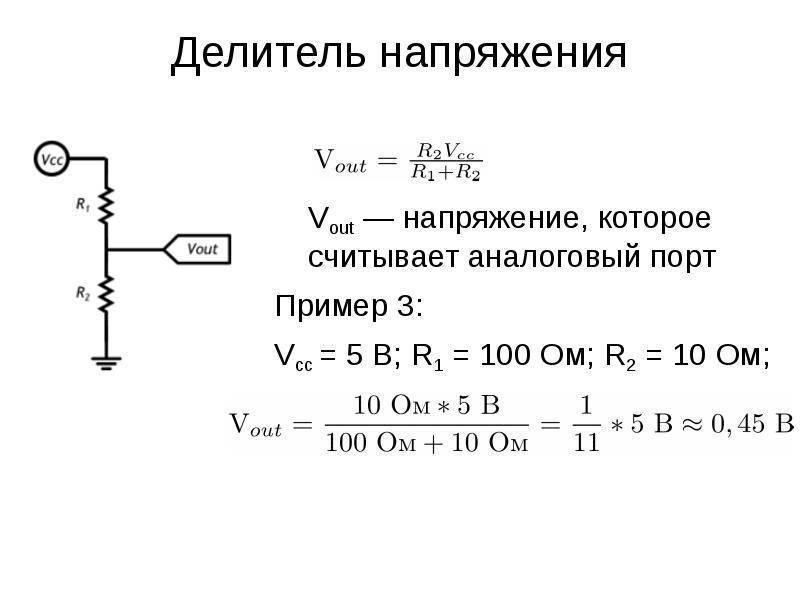
для получения необходимого заниженного напряжения в случаях, когда подключенная нагрузка потребляет небольшой ток (доли или единицы миллиампер). Примером подходящего использования является считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора .

Делитель не подходит

для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.

Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка на сами резисторы. Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое самой нагрузкой.

Если потребление тока нагрузкой неравномерно во времени, V out

также будет неравномерным.

Делитель напряжения применяется, если нужно получить заданное напряжение при условии стабилизированного питания. Сейчас мы поговорим о постоянном токе и резисторных делителях. О делителях с использованием конденсаторов, диодов, стабилитронов, индуктивностей и других элементов будет отдельная статья. Подпишитесь на новости, чтобы ее не пропустить. В конце для примера расскажу, как сделать делитель напряжения для осциллографа, чтобы снимать осциллограммы высокого напряжения.

Резисторные делители также могут применяться для уменьшения в заданное количество раз сигналов сложной формы. На делителях напряжения с регулируемым коэффициентом ослабления строятся, например, регуляторы громкости.

Вашему вниманию подборка материалов:

«Маленькие хитрости». Часть 4.

Формулы для радиолюбительских расчетов.

Каждый уважающий себя радио-мастер обязан знать формулы для расчета различных электрических величин. Ведь при ремонте электронных устройств или сборке электронных самоделок очень часто приходится проводить подобные расчеты. Не зная таких формул очень сложно и трудоемко, а порой и невозможно справиться с подобного рода задачей!

Как рассчитать емкость конденсатора, как рассчитать сопротивление резистора или узнать мощность устройства – в этом помогут формулы для радиолюбительских расчетов.

Первое, что нужно усвоить – ВСЕ ВЕЛЕЧИНЫ В ФОРМУЛАХ УКАЗЫВАЮТЬСЯ В АМПЕРАХ, ВОЛЬТАХ, ОМАХ, МЕТРАХ И КИЛОГЕРЦАХ.

Закон Ома.

Известный из школьного курса физики ЗАКОН ОМА. На нем строится большинство расчетов в радиоэлектронике. Закон Ома выражается в трех формулах:

I=U/R

U=IR

R=U/I

Где: I – сила тока (А), U – напряжение (В), R– сопротивление, имеющееся в цепи (Ом).

Теперь рассмотрим на практике применение формул в радиолюбительских расчетах.

Как рассчитать сопротивление гасящего резистора.

Сопротивление гасящего резистора рассчитывают по формуле: R=U/I

Где: U – излишек напряжения, который необходимо погасить (В), I – ток потребляемый цепью или устройством (А).

Как рассчитать мощность гасящего резистора.

Расчет мощности гасящего резистора проводят по формуле: P=I2R

Где I – ток потребляемый цепью или устройством (А), R– сопротивление резистора (Ом).

Как рассчитать напряжение падения на сопротивлении.

Напряжение падения на сопротивлении можно рассчитать по формуле: Uпад.=RI

Где R– сопротивление гасящего резистора (Ом), I– ток потребляемый устройством или цепью (А).

Как рассчитать ток потребляемый устройством или цепью.

Рассчитать ток потребляемый устройством или цепью можно по формуле: I=P/U

Где P– мощность устройства (Вт), U– напряжение питания устройства (В).

Как рассчитать мощность устройства в Вт.

Рассчитать мощность устройства в Вт можно по формуле: P=IU

Где I– ток потребляемый устройством (А), U– напряжение питания устройства (В).

Рассчитать длину радиоволны можно по формуле: ƛ=300000/ƒ

Где ƒ-частота в килогерцах ƛ- длинна волны в метрах.

Частоту радиосигнала можно рассчитать по формуле: ƒ=300000/ƛ

Где ƛ- длинна волны в метрах, ƒ – частота в килогерцах.

Как рассчитать номинальную выходную мощность звуковой частоты.

Рассчитать номинальную выходную мощность звуковоспроизводящего устройства (усилитель, проигрыватель и т.п.) можно по формуле: P=U2вых./ Rном.

Где U2 – напряжение звуковой частоты на нагрузке, R– номинальное сопротивление нагрузки.

И в завершении еще несколько формул. По этим формулам, ведут расчет сопротивления и емкости резисторов и конденсаторов в тех случаях, когда возникает необходимость в параллельном или последовательном их соединении.

Как рассчитать сопротивление двух параллельно включенных резисторов.

Расчет соединенных параллельно двух резисторов производят по формуле: R=R1R2/(R1+R2)

Где R1 и R2 — сопротивление первого и второго резистора соответственно (Ом).

Как рассчитать сопротивление более двух включенных параллельно резисторов.

Расчет сопротивления включенных параллельно более чем двух резисторов проводят по формуле: 1/R=1/R1+1/R2+1/Rn…

Где R1, R2, Rn… — сопротивление первого, второго и последующих резисторов соответственно (Ом).

Как рассчитать емкость включенных параллельно двух или более конденсаторов.

Расчет емкости соединенных параллельно нескольких конденсаторов проводят по формуле: C=C1+ C2+Cn…

Где C1 , C2 и Cn– емкость первого, второго и последующих конденсаторов соответственно (мФ).

Как рассчитать емкость включенных последовательно двух конденсаторов.

Расчет емкости двух соединенных последовательно конденсаторов проводят по формуле: C=C1 C2/C1+C2

Где C1 и C2 – емкость первого и второго конденсаторов соответственно (мФ).

Как рассчитать емкость включенных последовательно более двух конденсаторов.

Расчет емкости включенных последовательно более чем двух конденсаторов проводят по формуле: 1/C=1/C1+1/C2+1/Cn…

Где C1, C2 и Cn… — емкость первого, второго и последующих конденсаторов (мФ).

СЛЕДУЮЩИЙ МАТЕРИАЛ: Виртуальный осциллограф

Рекомендуем посмотреть:

Программы для радиолюбительских расчетов и измерений

Справочники по радиоэлектронике

Как работает делитель напряжения

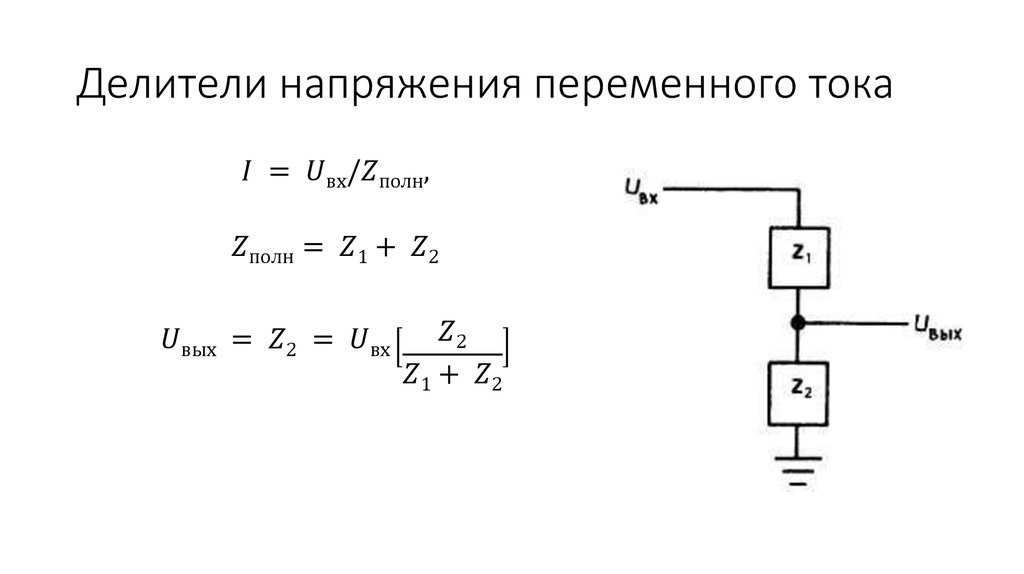
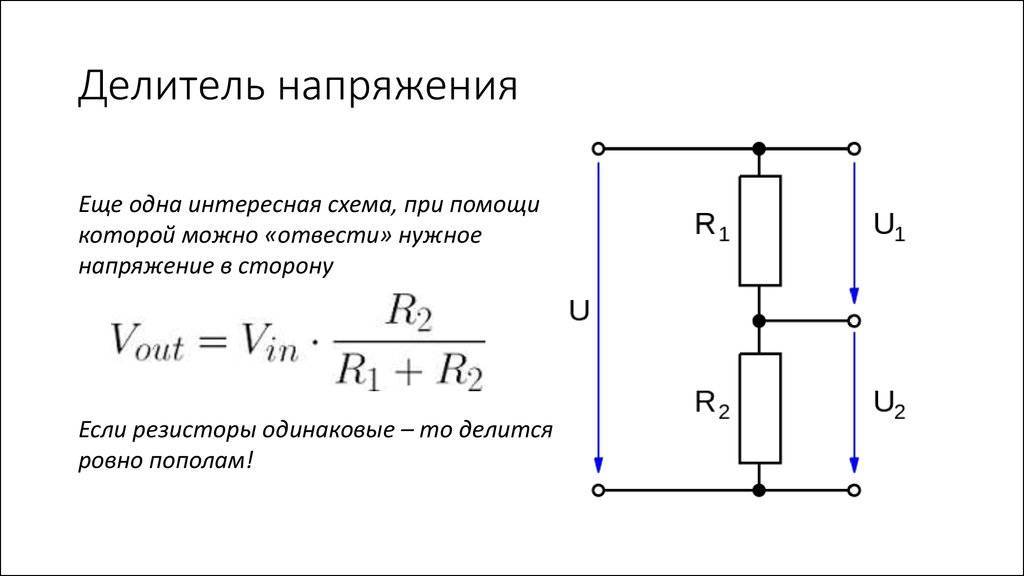
Делитель напряжения это устройство, осуществляющее регулировку выходного напряжения по отношению значения входного напряжения, в соответствии с коэффициентом передачи. То есть, из большего значения получается меньшее, а само напряжение бывает постоянным или переменным. Самая простая схема делителя напряжения состоит как минимум из двух сопротивлений. Если их сопротивления равны между собой, то и падения напряжения будут одинаковыми. Поэтому, по закону Ома напряжение на выходе прибора будет ровно в два раза ниже, чем на входе. В других случаях для расчетов падения напряжений используются формулы.

Основной функцией делителя напряжения в электрических цепях является снижение напряжения и получение нескольких его значений с фиксированными показателями на различных участках. Его основой служат резисторы или реактивные сопротивления в количестве два и более элементов.

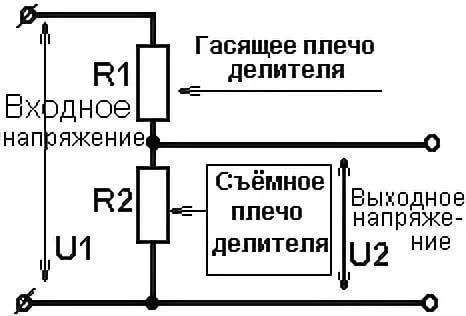
Простейший делитель представляется в виде двух участков цепи, называемых плечами. Верхним плечом считается участок между нулевой точкой и положительным напряжением, а нижним – участок между нулевой точкой и минусом. После того как определены исходные данные, можно сделать самый простой расчет делителя напряжения.

В качестве примера рассматриваются два резистора, соединенные последовательно. К ним подается напряжение U, которое может быть переменными или постоянным. После этого в действие вступает закон Ома, когда при последовательном соединении резисторов, общее сопротивление составит сумму их номиналов. В виде формы это будет выглядеть следующим образом: I = U/Rобщ, в которой Rобщ = R1+R2. Следовательно, I = U/(R1+R2).

Сила тока при последовательно соединенных резисторов, будет одинаковой на всех участках цепи. Если у каждого резистора имеется собственное значение сопротивления, то по закону Ома у них образуются совершенно разные напряжения. Сопротивлению R1 соответствует напряжение U1, а сопротивлению R2 – напряжение U2. В результате получается следующая ситуация, выраженная формулой I = U2/R2 = U1/R1 = U/(R1+R2). Для того, чтобы найти значения напряжений U1 и U2, необходимо выполнить такие действия: U1 = U x R1/(R1+R2) и U2 = U x R2/(R1+R2). Если правые части каждого уравнения сложить друг с другом, то в результате получится значение входящего напряжения U, состоящее из суммы напряжений U1 и U2, то есть U = U1 + U2. Это значит, что сумма падений напряжений на всех последовательно соединенных резисторах, будет равна напряжению источника питания, то есть входящему напряжению. Таким образом, данное выражение есть ни что иное, как формула делителя напряжения. Практически получается, что входящее напряжение U оказалось разделенным на два напряжения с собственными значениями – U1 и U2.

Во многих случаях необходимо, чтобы процесс разделения напряжения осуществлялся плавно. С этой целью был изобретен прибор – переменный резистор. Работа устройства происходит по установленной схеме. Два крайних контакта обладают постоянным сопротивлением, а сопротивление среднего контакта относительно крайних контактов будет изменяться в зависимости от направления вращения регулятора. С помощью переменных резисторов добавляется громкость в звуковых колонках, у радиоприемников и телевизоров старых марок.

Формула для расчета делителя напряжения

Начинающие радиолюбители часто задаются главным вопросом, как правильно рассчитать напряжение после резистора. Для этого необходимо знать, какой ток пойдет по цепи. В простейших схемах постоянного тока его вычисляют по линейному закону Ома. Формула расчета выглядит U=I*R, где:

• U — напряжение, В;
• I — ток, А;

В цепях с синусоидальным током, где присутствует реактивное сопротивление катушки или конденсатора, формула выглядит как R=1/(2*pi*f*L) и R=1/(2*pi*f*C) соответственно. В формуле использованы показатели:

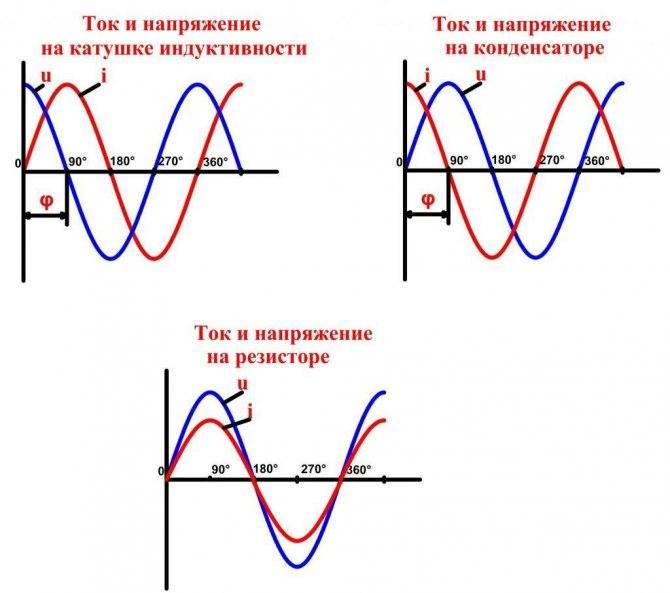График зависимости показателей от сопротивления

• R — реактивное сопротивление;
• R — сопротивление, Ом.
• pi — постоянное число Пи, равное 3,14;
• f — частота, Гц;
• L — индуктивность катушки, Генри;
• C — емкость конденсатора, Фарад.

Получив в расчетах внутреннюю резистивность элементов, далее можно воспользоваться линейной формулой для вычисления выходного значения.

На резисторе

В схеме делителя всегда участвует не меньше двух узлов нагрузки. Их коэффициенты могут быть равны другу, но и отличаться. Поэтому порой возникает необходимость получить номинал выходного вольтажа для каждого из них. Для этого используют всем известную формулу закона Ома: U=I*R.

Вам это будет интересно Все об скважности сигнала

После резистора

Для расчета показателя после резистора необходимо учитывать номиналы обоих элементов, так как они работают совместно друг с другом. Применив закон Ома, получается следующая формула: Uвых=Uпит*R1/(R1+R2), где:

• Uвых — вольтаж на выходе, В;
• Uпит — входной вольтаж, В;
• R1 — первый узел, Ом;
• R2 — второй узел, Ом.

Падение потенциалов за резистором рассчитывают для каждого узла в отдельности. То есть для второго элемента формула будет выглядеть так: Uвых=Uпит*R2/(R1+R2).

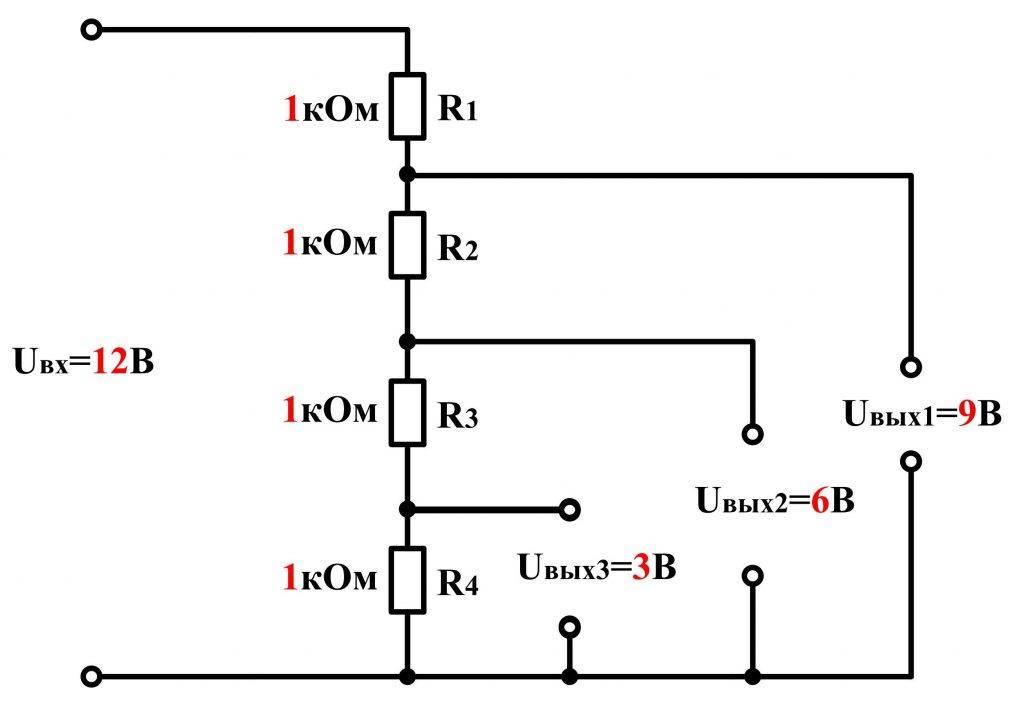
Делитель позволяет разработчикам получить несколько номинальных значений выходного напряжения от одного питающего источника. По этой причине схема получила широкое применение в электронике как в понижающих блоках питания, так и в качестве интегрированного узла электроцепи.

Примеры

Резистивный делитель

Рисунок 2: Простой резистивный делитель напряжения

Резистивный делитель — это случай, когда оба импеданса Z₁ и Z₂, являются чисто резистивными (рис. 2).

Подставляя Z₁ = R₁ и Z₂ = R₂ в предыдущее выражение дает:

Vотыт=р2р1+р2⋅Vяп{ Displaystyle V _ { mathrm {out}} = { frac {R_ {2}} {R_ {1} + R_ {2}}} cdot V _ { mathrm {in}}}

Если р₁ = р₂ тогда

Vотыт=12⋅Vяп{ Displaystyle V _ { mathrm {out}} = { frac {1} {2}} cdot V _ { mathrm {in}}}

Если V_из = 6В и V_в = 9 В (оба обычно используются напряжения), тогда:

VотытVяп=р2р1+р2=69=23{ displaystyle { frac {V _ { mathrm {out}}} {V _ { mathrm {in}}}} = { frac {R_ {2}} {R_ {1} + R_ {2}}} = { frac {6} {9}} = { frac {2} {3}}}

и решая с помощью алгебра, р₂ должно быть вдвое больше р₁.

Чтобы решить для R1:

р1=р2⋅VяпVотыт−р2=р2⋅(VяпVотыт−1){ displaystyle R_ {1} = { frac {R_ {2} cdot V _ { mathrm {in}}} {V _ { mathrm {out}}}} — R_ {2} = R_ {2} cdot left ({{ frac {V _ { mathrm {in}}} {V _ { mathrm {out}}}} — 1} right)}

Чтобы решить для R2:

р2=р1⋅1(VяпVотыт−1){ Displaystyle R_ {2} = R_ {1} cdot { frac {1} { left ({{ frac {V _ { mathrm {in}}} {V _ { mathrm {out}}}} — 1} right)}}}

Любое соотношение V_из/V_в больше 1 невозможно. То есть с помощью одних только резисторов невозможно ни инвертировать напряжение, ни увеличить V_из над V_в.

RC фильтр нижних частот

Рисунок 3: Резисторный / конденсаторный делитель напряжения

Рассмотрим делитель, состоящий из резистора и конденсатор как показано на рисунке 3.

Сравнивая с общим случаем, мы видим Z₁ = R и Z₂ импеданс конденсатора, определяемый

Z2=−jИксC=1jωC ,{ Displaystyle Z_ {2} = — mathrm {j} X _ { mathrm {C}} = { frac {1} { mathrm {j} omega C}} ,}

где X_C это реактивное сопротивление конденсатора, C — емкость конденсатора, j это мнимая единица, и ω (омега) это радианная частота входного напряжения.

Тогда этот делитель будет иметь соотношение напряжений:

VотытVяп=Z2Z1+Z2=1jωC1jωC+р=11+jωрC .{ displaystyle { frac {V _ { mathrm {out}}} {V _ { mathrm {in}}}} = { frac {Z _ { mathrm {2}}} {Z _ { mathrm {1}} + Z _ { mathrm {2}}}} = { frac { frac {1} { mathrm {j} omega C}} {{ frac {1} { mathrm {j} omega C}} + R}} = { frac {1} {1+ mathrm {j} omega RC}} .}

Продукт τ (тау) = RC называется постоянная времени схемы.

Соотношение затем зависит от частоты, в этом случае уменьшается с увеличением частоты. Эта схема, по сути, является базовой (первого порядка) фильтр нижних частот. Отношение содержит мнимое число и фактически содержит как амплитуду, так и сдвиг фазы информация о фильтре. Чтобы извлечь только отношение амплитуд, вычислите величина отношения, то есть:

|VотытVяп|=11+(ωрC)2 .{ displaystyle left | { frac {V _ { mathrm {out}}} {V _ { mathrm {in}}}} right | = { frac {1} { sqrt {1 + ( omega RC ) ^ {2}}}} .}

Индуктивный делитель

Индуктивные делители разделяют вход переменного тока по индуктивности:

Vотыт=L2L1+L2⋅Vяп{ displaystyle V _ { mathrm {out}} = { frac {L_ {2}} {L_ {1} + L_ {2}}} cdot V _ { mathrm {in}}}

Вышеприведенное уравнение предназначено для невзаимодействующих катушек индуктивности; взаимная индуктивность (как в автотрансформатор) изменит результаты.

Индуктивные делители делят вход постоянного тока в соответствии с сопротивлением элементов, как и в случае резистивного делителя, указанного выше.

Емкостной делитель

Емкостные делители не пропускают вход постоянного тока.

Для входа переменного тока простое емкостное уравнение:

Vотыт=C1C1+C2⋅Vяп{ Displaystyle V _ { mathrm {out}} = { frac {C_ {1}} {C_ {1} + C_ {2}}} cdot V _ { mathrm {in}}}

Любой ток утечки в емкостных элементах требует использования обобщенного выражения с двумя импедансами. Путем выбора параллельных элементов R и C в надлежащих пропорциях можно поддерживать одинаковый коэффициент деления в полезном диапазоне частот. Это принцип, применяемый в компенсированных осциллограф зонды для увеличения ширины полосы измерения.

Применение делителя напряжения на резисторах

В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.

Потенциометры

Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.

Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.

Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.

Резистивные датчики

Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.

Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).

Пример работы делителя напряжения на фоторезисторе.

Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.

Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

Тестер транзисторов / ESR-метр / генератор

Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…

Подробнее

https://youtube.com/watch?v=LnsDYvS93U0

Алгебраическая сумма разностей потенциалов

Закон напряжения по Густаву Кирхгофу – второй закон этого автора, используемый для анализа электрической цепи. Второй закон Кирхгофа гласит, что для последовательной замкнутой цепи алгебраическая сумма всех напряжений в круге любой замкнутой цепи равна нулю. Претензия связана с тем, что петля петли представляет собой замкнутый токопроводящий путь, где потери энергии исключены. Другими словами, алгебраическая сумма разностей потенциалов замкнутого контура теоретически равна нулю:

V = 0

Примечание. Термин «алгебраическая сумма» означает учет полярностей и знаков источников ЭДС, а также падения напряжения в цепи. Эта концепция закона Кирхгофа, известного как «сохранение энергии», как движение по контуру или замкнутому контуру, подтверждает логику возврата к началу цепи и к исходному потенциалу без потери напряжения во всей цепи.

Итак, вывод следует: при применении второго закона Кирхгофа к определенному элементу электрической цепи важно обращать особое внимание на алгебраические признаки падений напряжения на элементах (источниках ЭДС), иначе расчеты обернутся ошибкой

Одиночный контурный элемент — резистор

В качестве простого примера с резистором предположим, что ток течет в том же направлении, что и поток положительного заряда. В этом случае ток протекает через резистор от точки A к точке B. Действительно, от положительной клеммы к отрицательной. Следовательно, поскольку движение положительного заряда отмечается в направлении, аналогичном направлению протекания тока, на резистивном элементе будет зафиксировано падение потенциала, что приведет к падению отрицательного потенциала на резисторе (- I * R).

Если ток, протекающий из точки B в точку A, течет в направлении, противоположном потоку положительного заряда, вы заметите увеличение потенциала через резистивный элемент, поскольку происходит переход от отрицательного потенциала к положительному потенциалу, что дает падение напряжения. (+ I * R). Следовательно, чтобы правильно применить закон Кирхгофа к электрической цепи, необходимо точно определить направление полярности. Очевидно, знак падения напряжения на резисторе зависит от направления тока, протекающего через резистор.

Направление протекания тока в замкнутом контуре можно определять по или против часовой стрелки, и любой вариант допустим на выбор. Если выбранное направление отличается от фактического направления тока, соблюдение закона Кирхгофа будет правильным и действительным, но приведет к результату, когда алгебраический расчет имеет знак минус. Чтобы лучше понять эту концепцию, логично рассмотреть еще один пример с петлевой петлей на соответствие второму закону Кирхгофа.

Одиночный контур электрической цепи

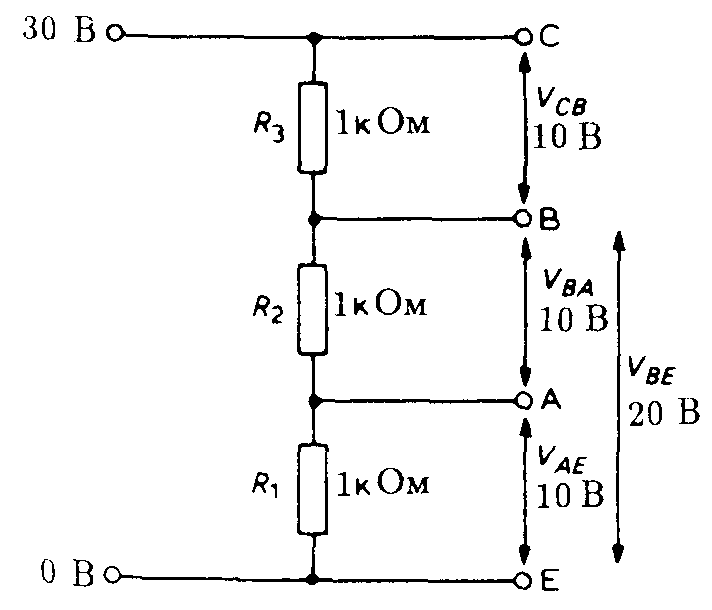
Второй закон Кирхгофа гласит, что алгебраическая сумма разностей потенциалов каждого замкнутого контура равна нулю. Демонстрационная схема действия Второго закона Кирхгофа для замкнутой цепи с двумя резисторами и источником ЭДС. Если принять условие, что два резистора R1 и R2 соединены последовательно, оба элемента являются частью одной цепи. В результате через каждый из резисторов протекает одинаковый ток.

Таким образом, падение напряжения на резисторе R1 = I * R1 и падение напряжения на резисторе R2 = I * R2 дают напряжение согласно второму закону Кирхгофа:

V = I * Rs

где: Rs = R1 + R2.

Очевидно, что применение второго закона Кирхгофа к одиночному замкнутому контуру дает формулу для эквивалента или импеданса для последовательной цепи. Допускается расширить эту формулу для нахождения значений капель потенциала по контурной окружности:

I = V / Rs

Vr1 = V * (R1 / R1 + R2)

Vr2 = V * (R2 / R1 + R2)

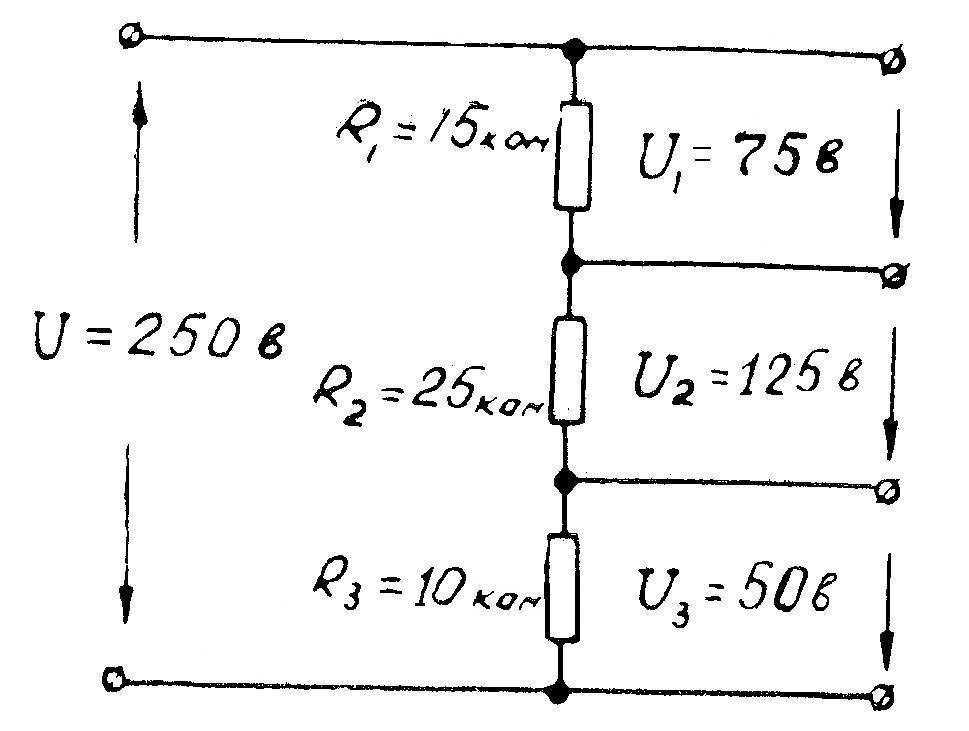
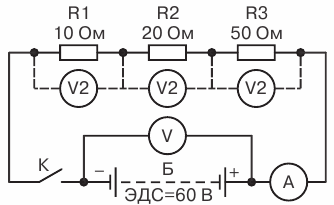
Есть три резистора с номинальным сопротивлением 10, 20, 30 Ом соответственно. Все три резистивных элемента соединены последовательно с батареей на 12 вольт.

Необходимо рассчитать:

• полное сопротивление,
• ток цепи,
• ток через каждый резистор,
• падение напряжения на каждом резисторе.

Рассчитываем полное сопротивление:

Ro = R1 + R2 + R3 = 10 Ом + 20 Ом + 30 Ом = 60 Ом

Ток цепи:

I = V / Ro = 12/60 = 0,2 А (200 мА)

Ток через каждый резистор:

I * R1 = I * R2 = I * R3 = 0,2 А (200 мА)

Потенциальное падение на каждом из резисторов:

VR1 = I * R1 = 0,2 * 10 = 2 В

VR2 = I * R2 = 0,2 * 20 = 4 В

VR3 = I * R3 = 0,2 * 30 = 6 В

Таким образом, действует Второй закон Кирхгофа, поскольку отдельные падения напряжения, обнаруживаемые по окружности замкнутого контура, в конечном итоге являются суммой напряжений.

Параллельное и последовательное соединение резисторов, решение задач

Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно. Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. На схеме присутствует параллельная и последовательная часть соединения элементов

Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?. Будет интересно Как прочитать обозначение (маркировку) резисторов

Будет интересно Как прочитать обозначение (маркировку) резисторов

Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.

Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.

Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше. Теперь образовалась ситуация — включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом

Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех. Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще

Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом

В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.

Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно. На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.

Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

• Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
• Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.

Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

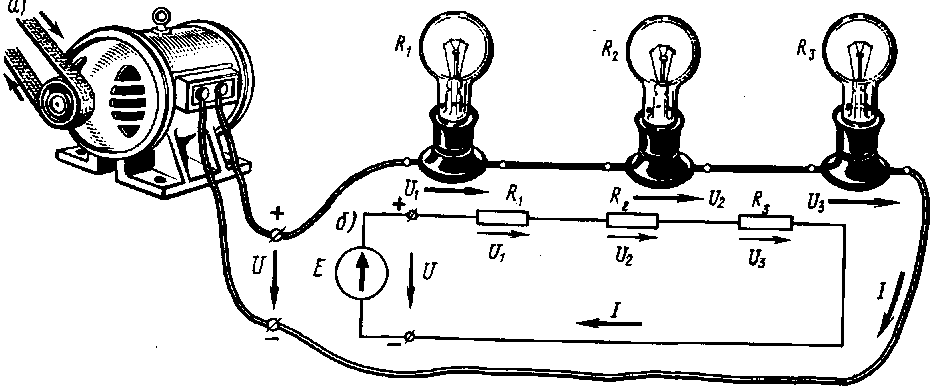
Типы подключений.

Как понизить напряжение с помощью резистора

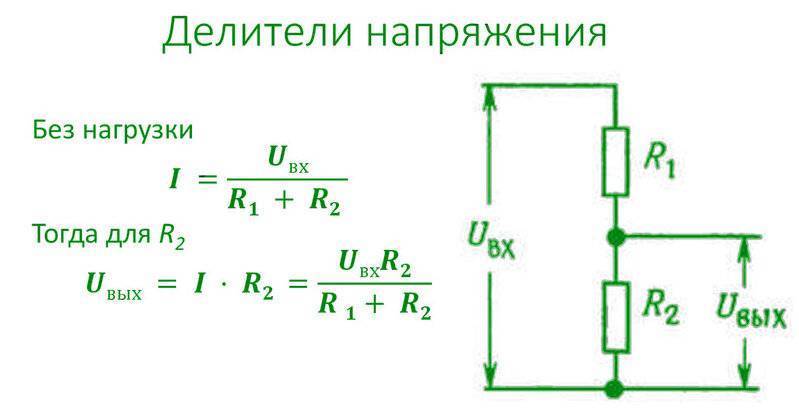
Чтобы нагрузка, которую требуется запитать, не сгорела, часто возникает необходимость снизить входное напряжение. Проще всего этого можно добиться, используя схему с двумя резисторами, более известную как делитель напряжения. Классическая схема выглядит так:

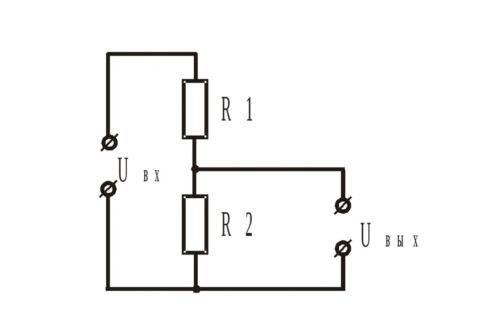
В этом случае напряжение подаётся на два резистора с использованием параллельного подключени, а на выходе его получают с одного. Подбор номиналов резисторов осуществляют по формуле так, чтобы напряжение, снимаемое на выходе, составляло какую-то часть от подаваемого. Расчет резистора для понижения напряжения можно воспользовавшись формулой, основанной на законе Ома:

U_вых= (U_вх*R₂)/(R₁+R₂), где

U_вх – напряжение на входе, В;

U_вых – напряжение на выходе, В

R₁ – показатель сопр. 1-ого резистора (Ом)

R₂ – показатель сопр. 2-ого элемента, (Ом)

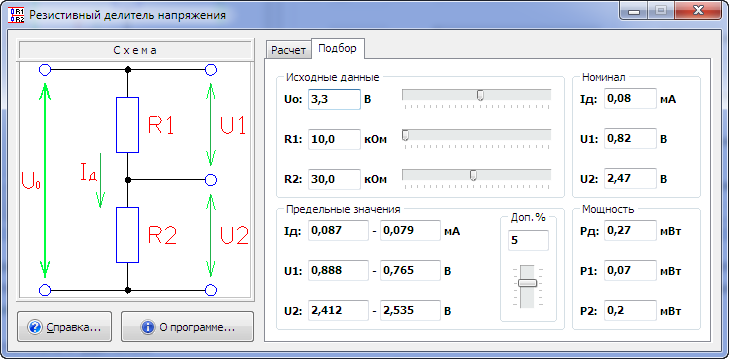
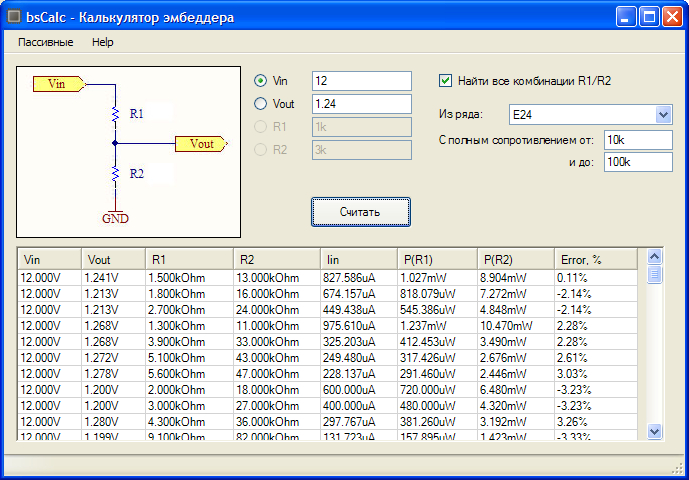
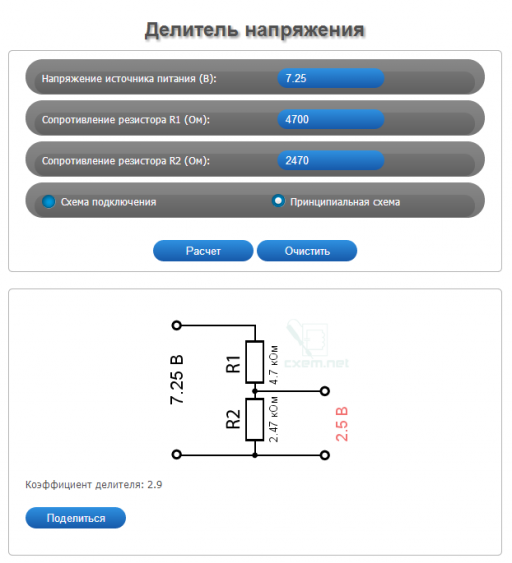
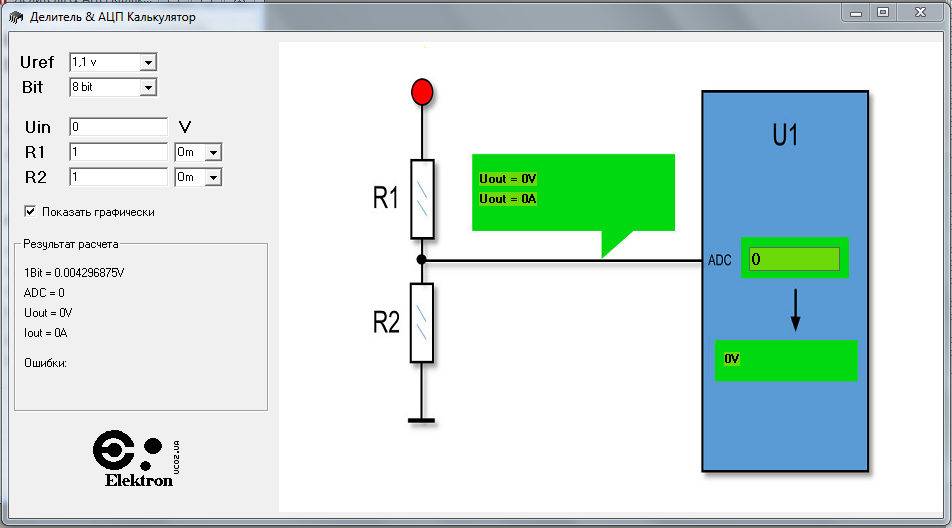
Подбор резистора для понижения напряжения

Для подбора нужного сопротивления резистора можно воспользоваться готовыми онлайн-калькуляторами или программами для моделирования работы электронных схем. Симуляторы электрических цепей способны не только рассчитать напряжение на выходе в зависимости от сопротивления элементов и способа их подключения, но и обладают функционалом, позволяющим визуализировать то, как падает ток и напряжение на резисторе. Например, приложение EveryCircuit позволяет изменять в схеме параметры элементов, выбирать скорость симуляции, получать данные в различных точках. При этом можно наблюдать за динамикой изменения значений, используя для ввода входных параметров вращающийся лимб в нижнем правом углу.

Существует ещё ряд бесплатных программ для эмуляции, позволяющие выполнить, в том числе, расчёт резистора при понижении напряжения, например:

• EasyEDA;
• Circuit Sims;
• DcAcLab;

и другие.

В статье мы ознакомились с понятием сопротивления, узнали о его единицах измерения, о маркировке резисторов, о программах эмулирующих работу цепи и облегчающих подбор нужного сопротивления, а также рассмотрели примеры расчёта падения напряжения на резисторе.